Quadratic

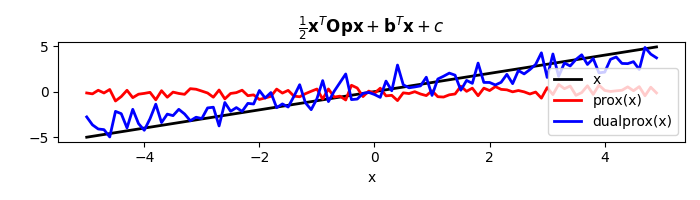
In this example we consider the proximal operator for a quadratic function:

\[\frac{1}{2} \mathbf{x}^T \mathbf{Op} \mathbf{x} + \mathbf{b}^T \mathbf{x} + c.\]

which is implemented by the pyproximal.Quadratic class.

import matplotlib.pyplot as plt
import numpy as np
import pylops

import pyproximal

plt.close("all")

To start with cosider the most complete case when both \(\mathbf{Op}\) and \(\mathbf{Op}\) are non-null.

x = np.arange(-5, 5, 0.1)
nx = len(x)

A = np.random.normal(0, 1, (nx, nx))
A = A.T @ A
c = 2.0
quad = pyproximal.Quadratic(Op=pylops.MatrixMult(A), b=np.ones_like(x), c=c, niter=500)
print("1/2 x^T Op x + b^T x + c: ", quad(x))

tau = 4
xp = quad.prox(x, tau)
xdp = quad.proxdual(x, tau)

plt.figure(figsize=(7, 2))
plt.plot(x, x, "k", lw=2, label="x")
plt.plot(x, xp, "r", lw=2, label="prox(x)")
plt.plot(x, xdp, "b", lw=2, label="dualprox(x)")
plt.xlabel("x")
plt.title(
    r"$\frac{1}{2} \mathbf{x}^T \mathbf{Op} \mathbf{x} + "
    r"\mathbf{b}^T \mathbf{x} + c$"
)
plt.legend()
plt.tight_layout()

1/2 x^T Op x + b^T x + c:  45293.7111248516

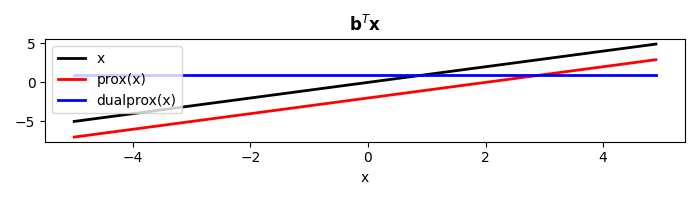
If we now assume that the operator \(\mathbf{Op}\) is null, the quadratic operator can be used to define the dot-product between \(\mathbf{x}\) and a vector \(\mathbf{b}\)

x = np.arange(-5, 5, 0.1)

dot = pyproximal.Quadratic(b=np.ones_like(x))
print("b^T x: ", quad(x))

tau = 2
xp = dot.prox(x, tau)
xdp = dot.proxdual(x, tau)

plt.figure(figsize=(7, 2))
plt.plot(x, x, "k", lw=2, label="x")
plt.plot(x, xp, "r", lw=2, label="prox(x)")
plt.plot(x, xdp, "b", lw=2, label="dualprox(x)")
plt.xlabel("x")
plt.title(r"$\mathbf{b}^T \mathbf{x}$")
plt.legend()
plt.tight_layout()

b^T x:  45293.7111248516

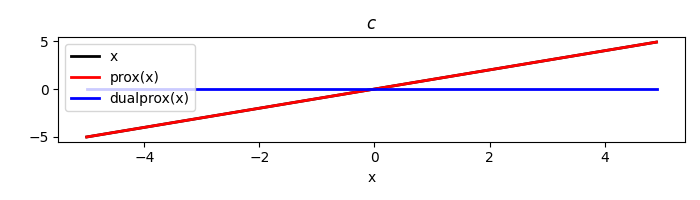
Finally if also \(\mathbf{b}\) is zero, the quadratic function reduces to a constant \(\mathbf{c}\) and its proximity operator becomes the vector \(\mathbf{x}\) itself.

x = np.arange(-5, 5, 0.1)

dot = pyproximal.Quadratic(c=5.0)
print("c: ", quad(x))

tau = 2
xp = dot.prox(x, tau)
xdp = dot.proxdual(x, tau)

plt.figure(figsize=(7, 2))
plt.plot(x, x, "k", lw=2, label="x")
plt.plot(x, xp, "r", lw=2, label="prox(x)")
plt.plot(x, xdp, "b", lw=2, label="dualprox(x)")
plt.xlabel("x")
plt.title(r"$c$")
plt.legend()
plt.tight_layout()

c:  45293.7111248516