Low-Rank completion via Matrix factorization

In this tutorial we will present another example of low-rank matrix completion. This time, however, we will not leverage SVD to find a low-rank representation of the matrix, instead we will look for two matrices whose inner product can represent the matrix we are after.

More specifically we will consider the following forward problem:

\[\mathbf{X},\mathbf{Y} = \argmin_{\mathbf{X}, \mathbf{Y}} \frac{1}{2} \|\mathbf{XY}-\mathbf{A}\|_F^2 + \delta_{\mathbf{X}\ge0} + \delta_{\mathbf{Y}\ge0}\]

where the non-negativity constraint (\(\delta_{\cdot \ge0}\)) is simply implemented using a Box proximal operator.

import numpy as np
import matplotlib.pyplot as plt
import pylops
import pyproximal

from scipy import misc

plt.close('all')
np.random.seed(10)

Let’s start by creating the matrix we want to factorize

n, m, k = 100, 90, 10
X = np.maximum(np.random.normal(0, 1, (n, k)), 0) + 1.
Y = np.maximum(np.random.normal(0, 1, (k, m)), 0) + 1.

A = X @ Y

We can now define the Box operators and the Low-Rank factorized operator. To do so we need some initial guess of \(\mathbf{X}\) and \(\mathbf{Y}\) that we create using the same distribution of the original ones.

nn1 = pyproximal.Box(lower=0)
nn2 = pyproximal.Box(lower=0)

Xin = np.maximum(np.random.normal(0, 1, (n, k)), 0) + 1.
Yin = np.maximum(np.random.normal(0, 1, (k, m)), 0) + 1.
Hop = pyproximal.utils.bilinear.LowRankFactorizedMatrix(Xin, Yin, A.ravel())

We are now ready to run the PALM algorithm

Xest, Yest = \
    pyproximal.optimization.palm.PALM(Hop, nn1, nn2, Xin.ravel(), Yin.ravel(),
                                      gammaf=2, gammag=2, niter=2000, show=True)
Xest, Yest = Xest.reshape(Xin.shape), Yest.reshape(Yin.shape)
Aest = Xest @ Yest

PALM algorithm
---------------------------------------------------------
Bilinear operator: <class 'pyproximal.utils.bilinear.LowRankFactorizedMatrix'>
Proximal operator (f): <class 'pyproximal.proximal.Box.Box'>
Proximal operator (g): <class 'pyproximal.proximal.Box.Box'>
gammaf = 2.000000e+00   gammaf = 2.000000e+00   niter = 2000

   Itn      x[0]       y[0]        f         g         H         ck         dk
     1  1.54505e+00  7.20e-01  1.00e+00  1.00e+00  3.76e+04  3.60e+03  3.72e+03
     2  1.58309e+00  5.86e-01  1.00e+00  1.00e+00  1.51e+04  3.56e+03  3.73e+03
     3  1.60203e+00  5.21e-01  1.00e+00  1.00e+00  9.35e+03  3.58e+03  3.74e+03
     4  1.61030e+00  4.92e-01  1.00e+00  1.00e+00  7.80e+03  3.59e+03  3.75e+03
     5  1.61340e+00  4.80e-01  1.00e+00  1.00e+00  7.32e+03  3.59e+03  3.75e+03
     6  1.61407e+00  4.77e-01  1.00e+00  1.00e+00  7.10e+03  3.59e+03  3.75e+03
     7  1.61360e+00  4.79e-01  1.00e+00  1.00e+00  6.96e+03  3.59e+03  3.75e+03
     8  1.61261e+00  4.83e-01  1.00e+00  1.00e+00  6.84e+03  3.59e+03  3.75e+03
     9  1.61137e+00  4.88e-01  1.00e+00  1.00e+00  6.73e+03  3.59e+03  3.75e+03
    10  1.61002e+00  4.94e-01  1.00e+00  1.00e+00  6.63e+03  3.59e+03  3.75e+03
   201  1.29414e+00  8.32e-01  1.00e+00  1.00e+00  2.65e+03  3.59e+03  3.75e+03
   401  9.24029e-01  7.10e-01  0.00e+00  1.00e+00  9.71e+02  3.59e+03  3.75e+03
   601  7.94781e-01  7.22e-01  0.00e+00  0.00e+00  3.89e+02  3.59e+03  3.76e+03
   801  7.68253e-01  7.50e-01  0.00e+00  0.00e+00  1.36e+02  3.58e+03  3.77e+03
  1001  7.73375e-01  7.53e-01  0.00e+00  0.00e+00  1.91e+01  3.58e+03  3.77e+03
  1201  7.77244e-01  7.52e-01  0.00e+00  0.00e+00  4.54e+00  3.57e+03  3.78e+03
  1401  7.81142e-01  7.50e-01  0.00e+00  0.00e+00  2.54e+00  3.57e+03  3.78e+03
  1601  7.85962e-01  7.48e-01  0.00e+00  0.00e+00  1.86e+00  3.56e+03  3.79e+03
  1801  7.91002e-01  7.45e-01  0.00e+00  0.00e+00  1.44e+00  3.56e+03  3.79e+03
  1992  7.95595e-01  7.42e-01  0.00e+00  0.00e+00  1.15e+00  3.56e+03  3.79e+03
  1993  7.95618e-01  7.42e-01  0.00e+00  0.00e+00  1.15e+00  3.56e+03  3.79e+03
  1994  7.95641e-01  7.42e-01  0.00e+00  0.00e+00  1.15e+00  3.56e+03  3.79e+03
  1995  7.95664e-01  7.42e-01  0.00e+00  0.00e+00  1.14e+00  3.56e+03  3.79e+03
  1996  7.95687e-01  7.42e-01  0.00e+00  0.00e+00  1.14e+00  3.56e+03  3.79e+03
  1997  7.95710e-01  7.42e-01  0.00e+00  0.00e+00  1.14e+00  3.56e+03  3.79e+03
  1998  7.95733e-01  7.42e-01  0.00e+00  0.00e+00  1.14e+00  3.56e+03  3.79e+03
  1999  7.95756e-01  7.42e-01  0.00e+00  0.00e+00  1.14e+00  3.56e+03  3.79e+03
  2000  7.95779e-01  7.42e-01  0.00e+00  0.00e+00  1.14e+00  3.56e+03  3.79e+03

Total time (s) = 0.33
---------------------------------------------------------

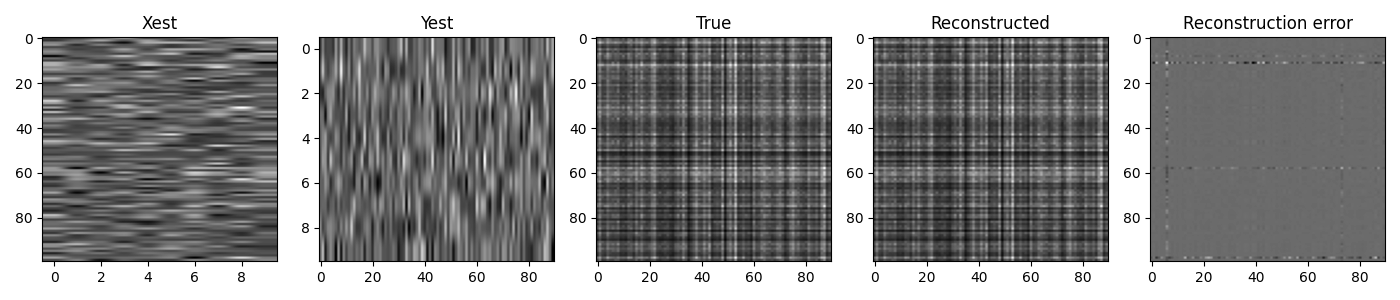
And finally we display the individual components and the reconstructed matrix

fig, axs = plt.subplots(1, 5, figsize=(14, 3))
axs[0].imshow(Xest, cmap='gray')
axs[0].set_title('Xest')
axs[0].axis('tight')
axs[1].imshow(Yest, cmap='gray')
axs[1].set_title('Yest')
axs[1].axis('tight')
axs[2].imshow(A, cmap='gray')
axs[2].set_title('True')
axs[2].axis('tight')
axs[3].imshow(Aest, cmap='gray')
axs[3].set_title('Reconstructed')
axs[3].axis('tight')
axs[4].imshow(A-Aest, cmap='gray')
axs[4].set_title('Reconstruction error')
axs[4].axis('tight')
fig.tight_layout()