Note
Go to the end to download the full example code
MRI Imaging and Segmentation of Brain#
This tutorial considers the well-known problem of MRI imaging, where given the availability of a sparsely sampled KK-spectrum, one is tasked to reconstruct the underline spatial luminosity of an object under observation. In this specific case, we will be using an example from Corona et al., 2019, Enhancing joint reconstruction and segmentation with non-convex Bregman iteration.
We first consider the imaging problem defined by the following cost functuon
where the operator \(\mathbf{A}\) performs a 2D-Fourier transform followed by sampling of the KK plane, \(\mathbf{x}\) is the object of interest and \(\mathbf{y}\) the set of available Fourier coefficients.
Once the model is reconstructed, we solve a second inverse problem with the aim of segmenting the retrieved object into \(N\) classes of different luminosity.
import numpy as np
import matplotlib.pyplot as plt
import pylops
from scipy.io import loadmat
import pyproximal
plt.close('all')
np.random.seed(10)
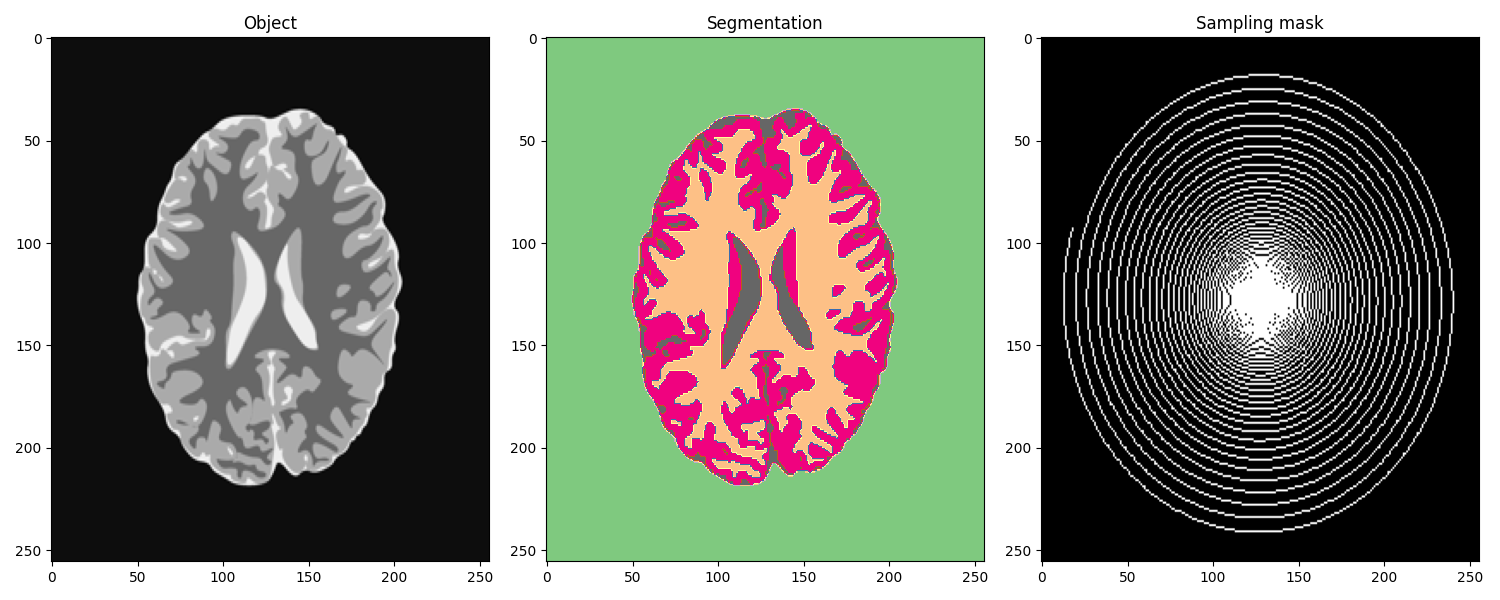
Let’s start by loading the data and the sampling mask
mat = loadmat('../testdata/brainphantom.mat')
mat1 = loadmat('../testdata/spiralsampling.mat')
gt = mat['gt']
seggt = mat['gt_seg']
sampling = mat1['samp']
sampling1 = np.fft.ifftshift(sampling)
fig, axs = plt.subplots(1, 3, figsize=(15, 6))
axs[0].imshow(gt, cmap='gray')
axs[0].axis('tight')
axs[0].set_title("Object")
axs[1].imshow(seggt, cmap='Accent')
axs[1].axis('tight')
axs[1].set_title("Segmentation")
axs[2].imshow(sampling, cmap='gray')
axs[2].axis('tight')
axs[2].set_title("Sampling mask")
plt.tight_layout()
We can now create the MRI operator
Fop = pylops.signalprocessing.FFT2D(dims=gt.shape)
Rop = pylops.Restriction(gt.size, np.where(sampling1.ravel() == 1)[0],
dtype=np.complex128)
Dop = Rop * Fop
# KK spectrum
GT = Fop * gt.ravel()
GT = GT.reshape(gt.shape)
# Data (Masked KK spectrum)
d = Dop * gt.ravel()
fig, axs = plt.subplots(1, 2, figsize=(12, 6))
axs[0].imshow(np.fft.fftshift(np.abs(GT)), vmin=0, vmax=1, cmap='gray')
axs[0].axis('tight')
axs[0].set_title("Spectrum")
axs[1].plot(np.fft.fftshift(np.abs(d)), 'k', lw=2)
axs[1].axis('tight')
axs[1].set_title("Masked Spectrum")
plt.tight_layout()
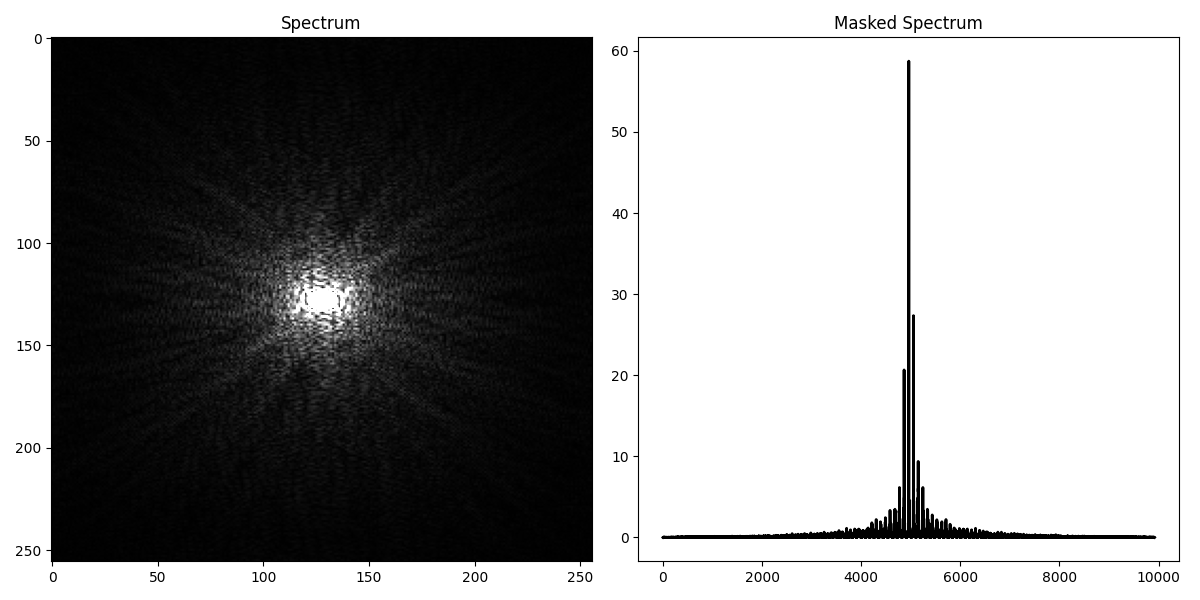
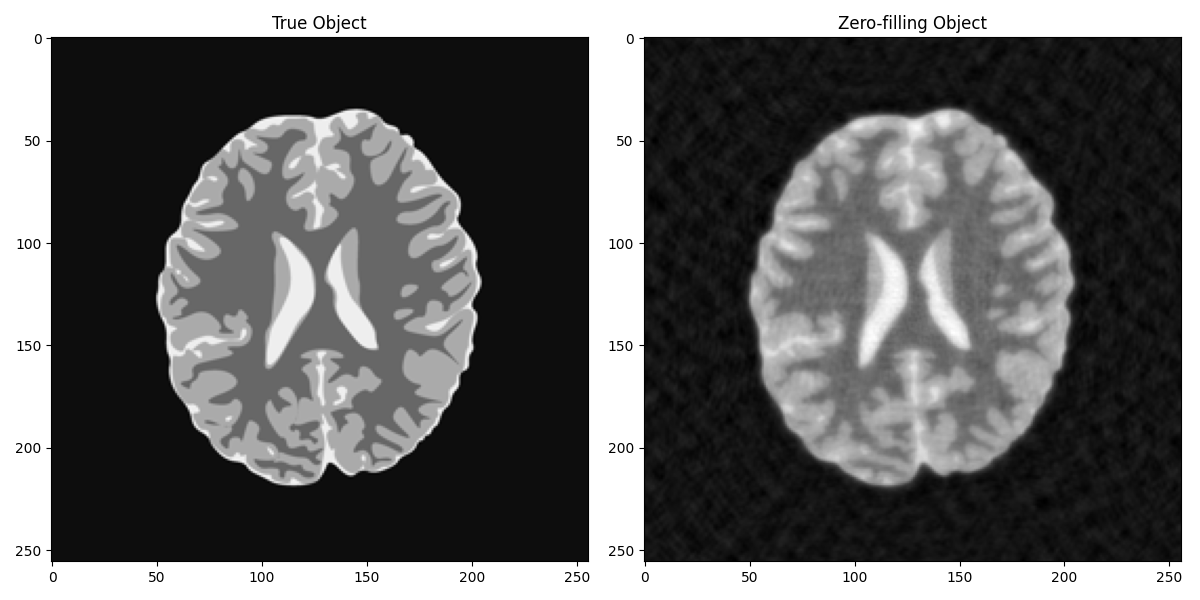
Let’s try now to reconstruct the object from its measurement. The simplest approach entails simply filling the missing values in the KK spectrum with zeros and applying inverse FFT.
GTzero = sampling1 * GT
gtzero = (Fop.H * GTzero).real
fig, axs = plt.subplots(1, 2, figsize=(12, 6))
axs[0].imshow(gt, cmap='gray')
axs[0].axis('tight')
axs[0].set_title("True Object")
axs[1].imshow(gtzero, cmap='gray')
axs[1].axis('tight')
axs[1].set_title("Zero-filling Object")
plt.tight_layout()
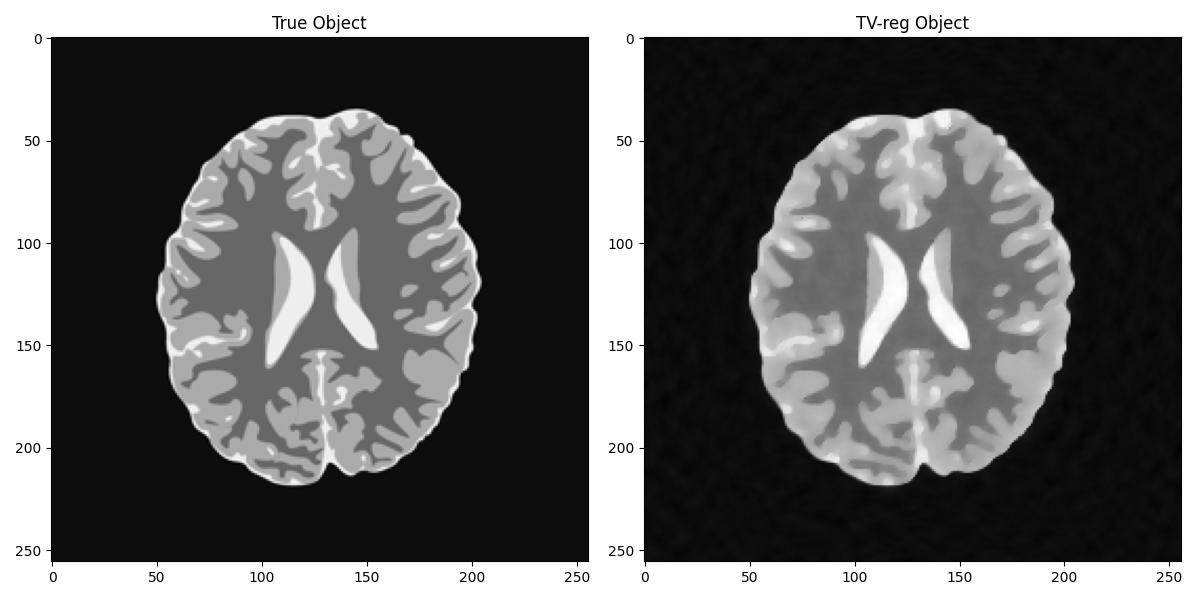
We can now do better if we introduce some prior information in the form of TV on the solution
with pylops.disabled_ndarray_multiplication():
sigma = 0.04
l1 = pyproximal.proximal.L21(ndim=2)
l2 = pyproximal.proximal.L2(Op=Dop, b=d.ravel(), niter=50, warm=True)
Gop = sigma * pylops.Gradient(dims=gt.shape, edge=True, kind='forward', dtype=np.complex128)
L = sigma ** 2 * 8
tau = .99 / np.sqrt(L)
mu = .99 / np.sqrt(L)
gtpd = pyproximal.optimization.primaldual.PrimalDual(l2, l1, Gop, x0=np.zeros(gt.size),
tau=tau, mu=mu, theta=1.,
niter=100, show=True)
gtpd = np.real(gtpd.reshape(gt.shape))
fig, axs = plt.subplots(1, 2, figsize=(12, 6))
axs[0].imshow(gt, cmap='gray')
axs[0].axis('tight')
axs[0].set_title("True Object")
axs[1].imshow(gtpd, cmap='gray')
axs[1].axis('tight')
axs[1].set_title("TV-reg Object")
plt.tight_layout()
Primal-dual: min_x f(Ax) + x^T z + g(x)
---------------------------------------------------------
Proximal operator (f): <class 'pyproximal.proximal.L2.L2'>
Proximal operator (g): <class 'pyproximal.proximal.L21.L21'>
Linear operator (A): <class 'pylops.linearoperator._ScaledLinearOperator'>
Additional vector (z): None
tau = 8.750446417183525 mu = 8.750446417183525
theta = 1.00 niter = 100
Itn x[0] f g z^x J = f + g + z^x
/home/docs/checkouts/readthedocs.org/user_builds/pyproximal/envs/stable/lib/python3.9/site-packages/pyproximal/optimization/primaldual.py:169: ComplexWarning: Casting complex values to real discards the imaginary part
msg = '%6g %12.5e %10.3e %10.3e %10.3e %10.3e' % \
1 4.16746e-02 4.132e+01 5.643e+01 0.000e+00 9.775e+01
2 4.07823e-02 5.185e-01 6.082e+01 0.000e+00 6.134e+01
3 3.45600e-02 1.293e-01 6.055e+01 0.000e+00 6.068e+01
4 2.82259e-02 2.128e-01 5.990e+01 0.000e+00 6.011e+01
5 2.31727e-02 3.271e-01 5.924e+01 0.000e+00 5.956e+01
6 1.98898e-02 4.624e-01 5.861e+01 0.000e+00 5.907e+01
7 1.83837e-02 6.164e-01 5.800e+01 0.000e+00 5.862e+01
8 1.83766e-02 7.874e-01 5.743e+01 0.000e+00 5.822e+01
9 1.94602e-02 9.740e-01 5.688e+01 0.000e+00 5.786e+01
10 2.12040e-02 1.175e+00 5.636e+01 0.000e+00 5.754e+01
11 2.32695e-02 1.387e+00 5.585e+01 0.000e+00 5.724e+01
21 4.46572e-02 2.942e+00 5.401e+01 0.000e+00 5.696e+01
31 4.41414e-02 3.808e+00 5.324e+01 0.000e+00 5.705e+01
41 2.52806e-02 4.741e+00 4.975e+01 0.000e+00 5.449e+01
51 3.33766e-02 5.463e+00 4.941e+01 0.000e+00 5.487e+01
61 4.13994e-02 5.864e+00 4.996e+01 0.000e+00 5.583e+01
71 6.61764e-02 6.079e+00 4.994e+01 0.000e+00 5.602e+01
81 3.41396e-02 6.203e+00 4.918e+01 0.000e+00 5.539e+01
91 4.35365e-02 6.289e+00 4.886e+01 0.000e+00 5.515e+01
92 4.45981e-02 6.299e+00 4.871e+01 0.000e+00 5.501e+01
93 4.62498e-02 6.306e+00 4.857e+01 0.000e+00 5.487e+01
94 4.73891e-02 6.313e+00 4.844e+01 0.000e+00 5.476e+01
95 4.80258e-02 6.319e+00 4.831e+01 0.000e+00 5.463e+01
96 4.78933e-02 6.326e+00 4.817e+01 0.000e+00 5.449e+01
97 4.80336e-02 6.332e+00 4.809e+01 0.000e+00 5.442e+01
98 4.76974e-02 6.338e+00 4.798e+01 0.000e+00 5.432e+01
99 4.66103e-02 6.342e+00 4.795e+01 0.000e+00 5.429e+01
100 4.59480e-02 6.346e+00 4.809e+01 0.000e+00 5.444e+01
Total time (s) = 5.57
---------------------------------------------------------
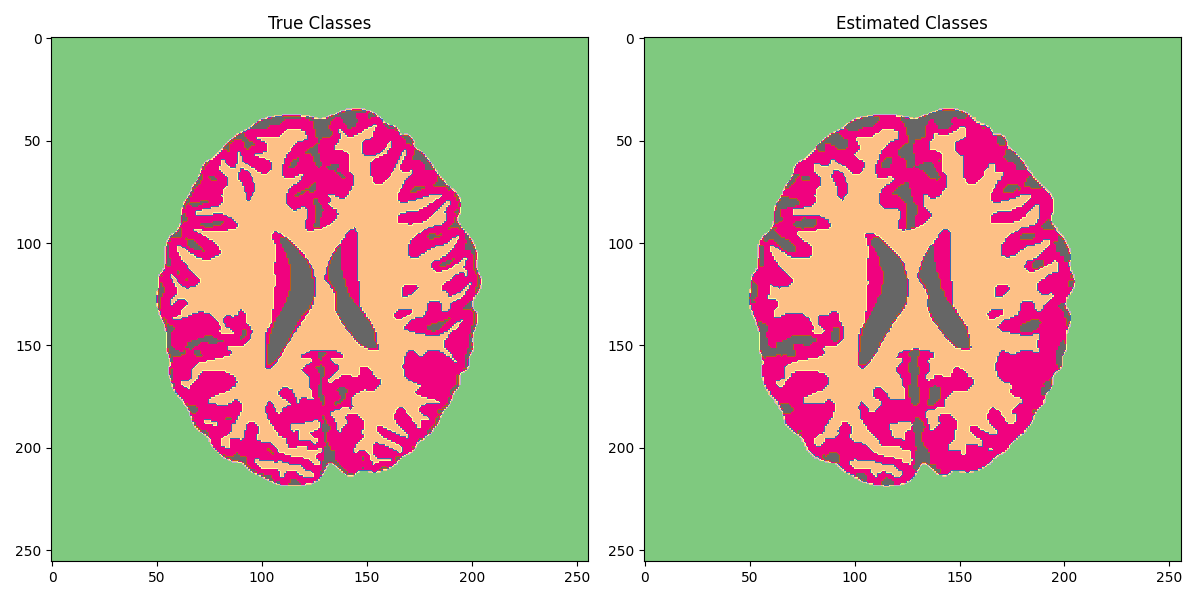
Finally we segment our reconstructed model into 4 classes.
cl = np.array([0.01, 0.43, 0.65, 0.8])
ncl = len(cl)
segpd_prob, segpd = \
pyproximal.optimization.segmentation.Segment(gtpd, cl, 1., 0.001,
niter=10, show=True,
kwargs_simplex=dict(engine='numba'))
fig, axs = plt.subplots(1, 2, figsize=(12, 6))
axs[0].imshow(seggt, cmap='Accent')
axs[0].axis('tight')
axs[0].set_title("True Classes")
axs[1].imshow(segpd, cmap='Accent')
axs[1].axis('tight')
axs[1].set_title("Estimated Classes")
plt.tight_layout()
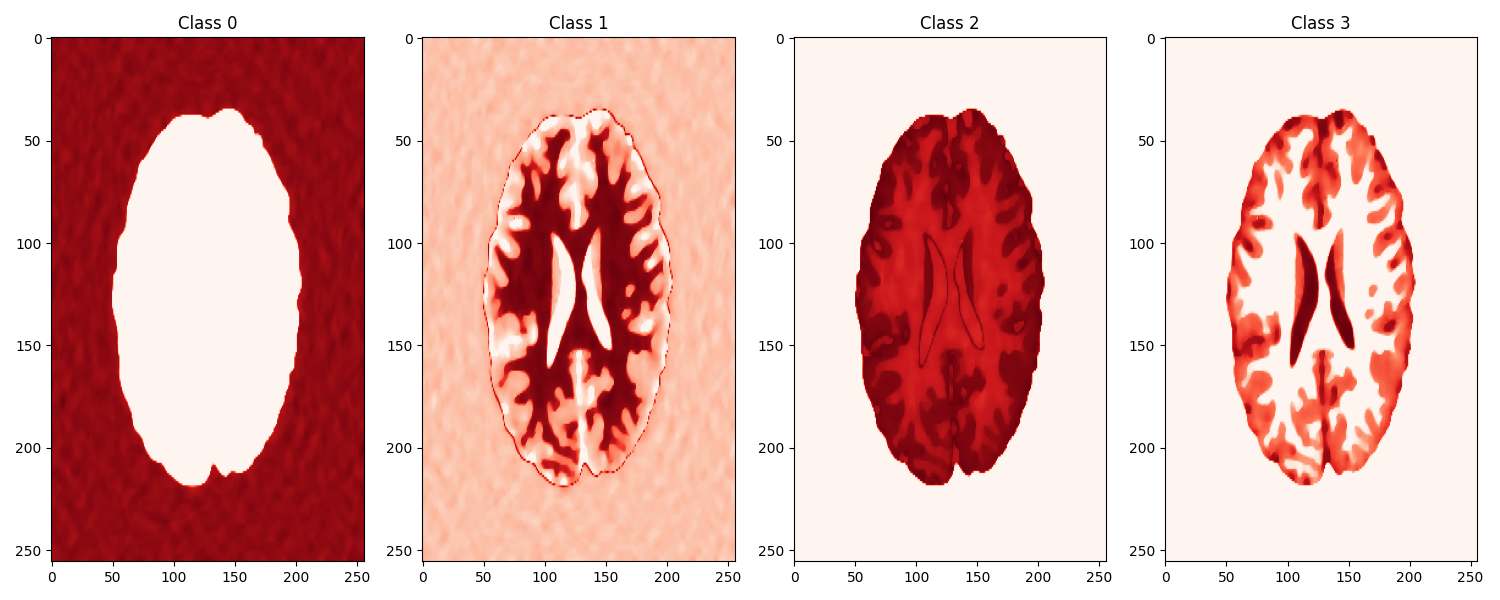
fig, axs = plt.subplots(1, 4, figsize=(15, 6))
for i, ax in enumerate(axs):
ax.imshow(segpd_prob[:, i].reshape(gt.shape), cmap='Reds')
axs[i].axis('tight')
axs[i].set_title(f"Class {i}")
plt.tight_layout()
Primal-dual: min_x f(Ax) + x^T z + g(x)
---------------------------------------------------------
Proximal operator (f): <class 'pyproximal.proximal.Simplex._Simplex_numba'>
Proximal operator (g): <class 'pyproximal.proximal.VStack.VStack'>
Linear operator (A): <class 'pylops.basicoperators.blockdiag.BlockDiag'>
Additional vector (z): vector
tau = 1.0 mu = 0.125
theta = 1.00 niter = 10
Itn x[0] f g z^x J = f + g + z^x
1 3.84637e-01 1.000e+00 6.352e-01 4.608e+03 4.610e+03
2 5.02754e-01 1.000e+00 9.414e-01 2.781e+03 2.783e+03
3 5.87047e-01 1.000e+00 1.145e+00 2.025e+03 2.027e+03
4 6.45121e-01 1.000e+00 1.259e+00 1.551e+03 1.553e+03
5 6.81068e-01 1.000e+00 1.420e+00 1.390e+03 1.392e+03
6 7.17043e-01 1.000e+00 1.572e+00 1.238e+03 1.240e+03
7 7.53036e-01 1.000e+00 1.719e+00 1.091e+03 1.094e+03
8 7.89040e-01 1.000e+00 1.846e+00 9.524e+02 9.552e+02
9 8.25058e-01 1.000e+00 1.963e+00 8.292e+02 8.322e+02
10 8.61091e-01 1.000e+00 2.087e+00 7.134e+02 7.165e+02
Total time (s) = 72.31
---------------------------------------------------------
Total running time of the script: (1 minutes 20.691 seconds)