Group sparsity

This notebooks considers the problem of jointly interpolating N (e.g., 2) signals with sparse representation in the frequency domain and shows the importance of applying a group sparsity constraint by means of the pyproximal.proximal.L01Ball proximal operator.

Given the following problem:

\[[\mathbf{y}_1^T, \mathbf{y}_2^T,\ldots,\mathbf{y}_N^T]^T = diag(\mathbf{R}, \mathbf{R}, ..., \mathbf{R}) [\mathbf{x}_1^T, \mathbf{x}_2^T, \ldots,\mathbf{x}_N^T]^T \rightarrow \mathbf{y}=\mathbf{R}_N\mathbf{x} ,\]

we aim to find a solution to this objective function:

\[J = \frac{1}{2} ||\mathbf{y} - \mathbf{R}_N \mathbf{x}||_2^2 \; s.t. ||\mathbf{X}||_{0,1} < K\]

where \(\mathbf{X}\) is a matrix whose rows are represented by the different signals \(\mathbf{x}_i\), and the \(L_{0,1}\) norm computes the number of non-zero elements of a vector whose elements are the $L_1$ norm of each column of \(\mathbf{X}\).

import numpy as np
import matplotlib.pyplot as plt
import pylops

import pyproximal

plt.close('all')
np.random.seed(10)

Let’s first create 2 signals in the frequency domain composed by the superposition of 3 sinusoids with different frequencies.

ifreqs = [4, 8, 11]
amps1 = [1.0, 0.2, 0.5]
amps2 = [3.0, 3.0, 2.0]

N = 2 ** 8
nfft = N
dt = 0.004
t = np.arange(N) * dt
f = np.fft.rfftfreq(nfft, dt)

FFTop = 10 * pylops.signalprocessing.FFT(N, nfft=nfft, real=True)

X1 = np.zeros(nfft // 2 + 1, dtype='complex128')
X2 = np.zeros(nfft // 2 + 1, dtype='complex128')
X1[ifreqs] = amps1
X2[ifreqs] = amps2

x1 = FFTop.H * X1
x2 = FFTop.H * X2

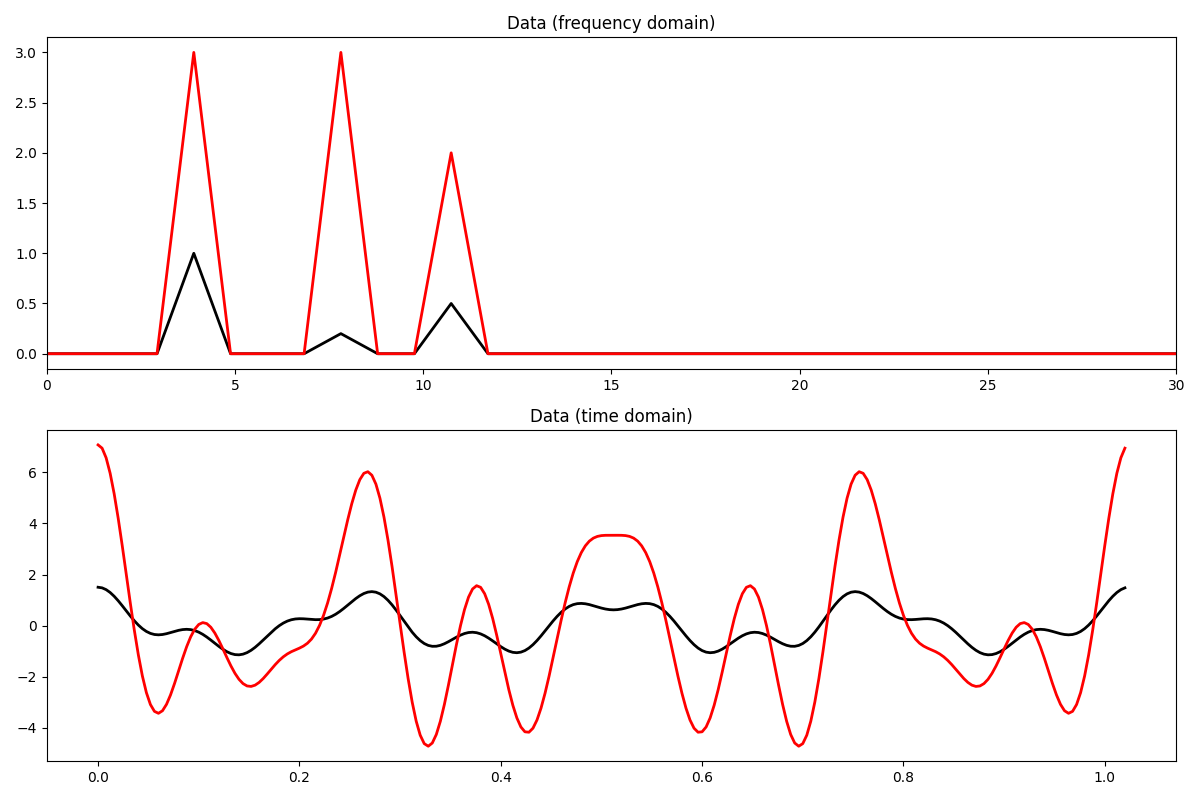
fig, axs = plt.subplots(2, 1, figsize=(12, 8))
axs[0].plot(f, np.abs(X1), 'k', lw=2)
axs[0].plot(f, np.abs(X2), 'r', lw=2)
axs[0].set_xlim(0, 30)
axs[0].set_title('Data (frequency domain)')
axs[1].plot(t, x1, 'k', lw=2)
axs[1].plot(t, x2, 'r', lw=2)
axs[1].set_title('Data (time domain)')
axs[1].axis('tight')
plt.tight_layout()

We now define the locations at which the signals will be sampled. The first signal is severely subsampled (10% of available samples), whilst the second dataset retains 60% of its samples. This choice is made on purpose to see if group sparsity could help interpolating the first signal by leveraging the fact that it is easier to interpolate the second signal

np.random.seed(10)

perc_subsampling = (0.1, 0.6)
Nsub1, Nsub2 = int(np.round(N * perc_subsampling[0])), int(np.round(N * perc_subsampling[1]))
iava1 = np.sort(np.random.permutation(np.arange(N))[:Nsub1])
iava2 = np.sort(np.random.permutation(np.arange(N))[:Nsub2])

# Create restriction operator
Rop1 = pylops.Restriction(N, iava1, dtype='float64')
Rop2 = pylops.Restriction(N, iava2, dtype='float64')

y1 = Rop1 * x1
y2 = Rop2 * x2

Op1 = Rop1 * FFTop.H
Op2 = Rop2 * FFTop.H

X1adj = Op1.H * y1
X2adj = Op2.H * y2

Let’s try to interpolate the first signal

L = np.abs((Op1.H * Op1).eigs(1)[0])
eps = 1  # not used given that a projection is used as regularizer
niter = 400
tau = 0.95 / L

l0 = pyproximal.proximal.L0Ball(3)
l2 = pyproximal.proximal.L2(Op=Op1, b=y1)
X1est = pyproximal.optimization.primal.ProximalGradient(
    l2, l0, tau=tau, x0=np.zeros(nfft // 2 + 1, dtype='complex128'),
    epsg=eps, niter=niter, acceleration='fista', show=False)
x1est = FFTop.H * X1est

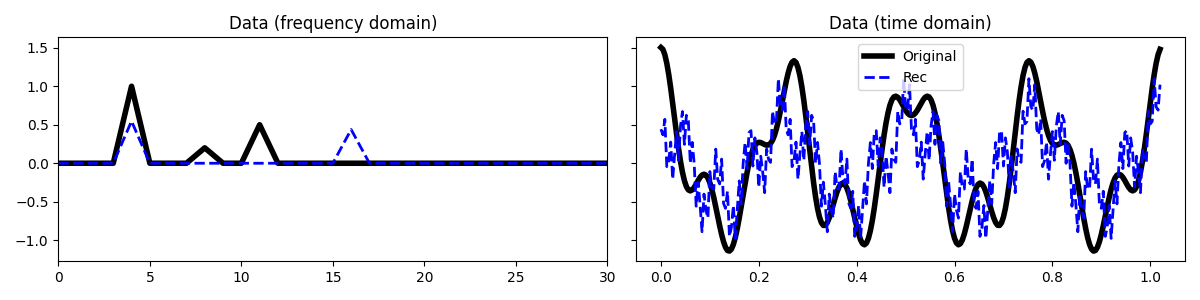
fig, axs = plt.subplots(1, 2, sharey=True, figsize=(12, 3))
axs[0].plot(np.abs(X1), 'k', lw=4, label='Original')
axs[0].plot(np.abs(X1est), '--b', lw=2, label='Rec')
axs[0].set_title('Data (frequency domain)')
axs[0].set_xlim(0, 30)
axs[1].plot(t, x1, 'k', lw=4, label='Original')
axs[1].plot(t, x1est, '--b', lw=2, label='Rec')
axs[1].set_title('Data (time domain)')
axs[1].legend()
plt.tight_layout()

And now we interpolate the two signals together

Opp = pylops.BlockDiag([Op1, Op2])
yy = np.hstack([y1, y2])

L = np.abs((Opp.H * Opp).eigs(1)[0])
eps = 1  # not used given that a projection is used as regularizer
niter = 400
tau= 0.99 / L

l0 = pyproximal.proximal.L01Ball(ndim=2, radius=4)
l2 = pyproximal.proximal.L2(Op=Opp, b=yy)

XXest = pyproximal.optimization.primal.ProximalGradient(
    l2, l0, tau=tau, x0=np.zeros(2*(nfft // 2 + 1), dtype='complex128'),
    epsg=eps, niter=niter, acceleration='fista', show=False)

X1est, X2est = XXest[:FFTop.shape[0]], XXest[FFTop.shape[0]:]
x1est = FFTop.H * X1est
x2est = FFTop.H * X2est

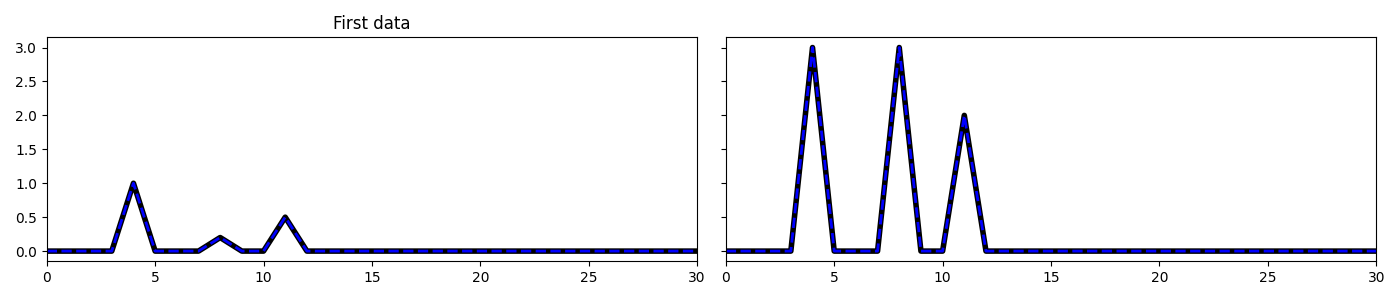
fig, axs = plt.subplots(1, 2, sharey=True, figsize=(14, 3))
axs[0].plot(np.abs(X1), 'k', lw=4, label='Original')
axs[0].plot(np.abs(X1est), '--b', lw=2, label='Rec')
axs[0].set_title('First data')
axs[1].plot(np.abs(X2), 'k', lw=4)
axs[1].plot(np.abs(X2est), '--b', lw=2)
axs[0].set_xlim(0, 30)
axs[1].set_xlim(0, 30)
plt.tight_layout()

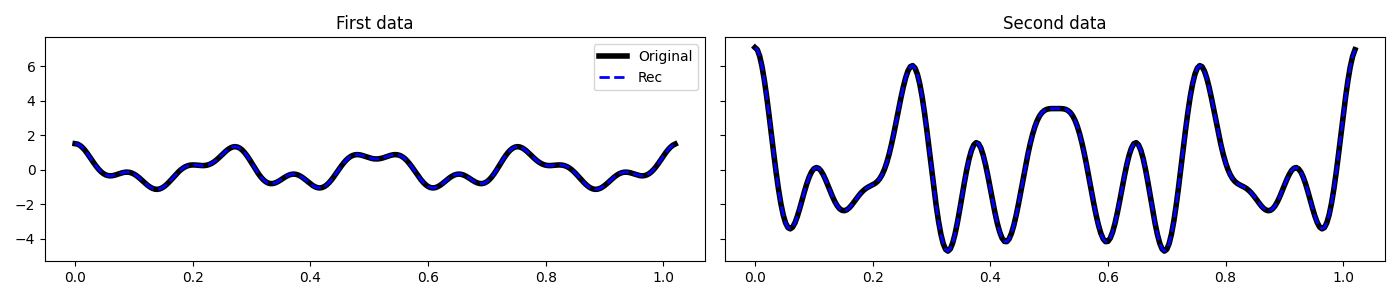
fig, axs = plt.subplots(1, 2, sharey=True, figsize=(14, 3))
axs[0].plot(t, x1, 'k', lw=4, label='Original')
axs[0].plot(t, x1est, '--b', lw=2, label='Rec')
axs[0].set_title('First data')
axs[0].legend()
axs[1].plot(t, x2, 'k', lw=4)
axs[1].plot(t, x2est, '--b', lw=2)
axs[1].set_title('Second data')
plt.tight_layout()

• 
• 

/home/docs/checkouts/readthedocs.org/user_builds/pyproximal/envs/stable/lib/python3.9/site-packages/numpy/lib/shape_base.py:260: ComplexWarning: Casting complex values to real discards the imaginary part
  arr[_make_along_axis_idx(arr_shape, indices, axis)] = values