IHT, ISTA, FISTA, AA-ISTA, and TWIST for Compressive sensing

In this example we want to compare five popular solvers in compressive sensing problem, namely IHT, ISTA, FISTA, AA-ISTA, and TwIST. The first three can be implemented using the same solver, namely the pyproximal.optimization.primal.ProximalGradient, whilst the latter two are implemented using the pyproximal.optimization.primal.AndersonProximalGradient and pyproximal.optimization.primal.TwIST solvers, respectively

The IHT solver tries to solve the following unconstrained problem with a L0Ball regularization term:

\[J = \|\mathbf{d} - \mathbf{Op} \mathbf{x}\|_2 \; s.t. \; \|\mathbf{x}\|_0 \le K\]

The other solvers try instead to solve an unconstrained problem with a L1 regularization term:

\[J = \|\mathbf{d} - \mathbf{Op} \mathbf{x}\|_2 + \epsilon \|\mathbf{x}\|_1\]

however their convergence speed is different, which is something we want to focus in this tutorial.

import numpy as np
import matplotlib.pyplot as plt

import pylops
import pyproximal

plt.close('all')
np.random.seed(0)

def callback(x, pf, pg, eps, cost):
    cost.append(pf(x) + eps * pg(x))

Let’s start by creating a dense mixing matrix and a sparse signal. Note that the mixing matrix leads to an underdetermined system of equations (\(N < M\)) so being able to add some extra prior information regarding the sparsity of our desired model is essential to be able to invert such a system.

N, M = 15, 20
A = np.random.randn(N, M)
A = A / np.linalg.norm(A, axis=0)
Aop = pylops.MatrixMult(A)

x = np.random.rand(M)
x[x < 0.9] = 0
y = Aop * x

We try now to recover the sparse signal with our 4 different solvers

L = np.abs((Aop.H * Aop).eigs(1)[0])
tau = 0.95 / L
eps = 5e-3
maxit = 300

# IHT
l0 = pyproximal.proximal.L0Ball(3)
l2 = pyproximal.proximal.L2(Op=Aop, b=y)
costf1 = []
x_iht = pyproximal.optimization.primal.ProximalGradient(l2, l0, tau=tau, x0=np.zeros(M),
                       epsg=eps, niter=maxit, acceleration='fista', show=False)

# ISTA
l1 = pyproximal.proximal.L1()
l2 = pyproximal.proximal.L2(Op=Aop, b=y)
costi = []
x_ista = \
    pyproximal.optimization.primal.ProximalGradient(l2, l1, tau=tau, x0=np.zeros(M),
                                                    epsg=eps, niter=maxit, show=False,
                                                    callback=lambda x: callback(x, l2, l1, eps, costi))
niteri = len(costi)

# FISTA
l1 = pyproximal.proximal.L1()
l2 = pyproximal.proximal.L2(Op=Aop, b=y)
costf = []
x_fista = \
    pyproximal.optimization.primal.ProximalGradient(l2, l1, tau=tau, x0=np.zeros(M),
                                                    epsg=eps, niter=maxit, acceleration='fista', show=False,
                                                    callback=lambda x: callback(x, l2, l1, eps, costf))
niterf = len(costf)

# Anderson accelerated ISTA
l1 = pyproximal.proximal.L1()
l2 = pyproximal.proximal.L2(Op=Aop, b=y)
costa = []
x_ander = \
    pyproximal.optimization.primal.AndersonProximalGradient(l2, l1, tau=tau, x0=np.zeros(M),
                                                            epsg=eps, niter=maxit,
                                                            nhistory=5, show=False,
                                                            callback=lambda x: callback(x, l2, l1, eps, costa))
nitera = len(costa)


# TWIST (Note that since the smallest eigenvalue is zero, we arbitrarily
# choose a small value for the solver to converge stably)
l1 = pyproximal.proximal.L1(sigma=eps)
eigs = (Aop.H * Aop).eigs()
eigs = (np.abs(eigs[0]), 5e-1)
x_twist, costt = \
    pyproximal.optimization.primal.TwIST(l1, Aop, y, eigs=eigs,
                                         x0=np.zeros(M), niter=maxit,
                                         show=False, returncost=True)

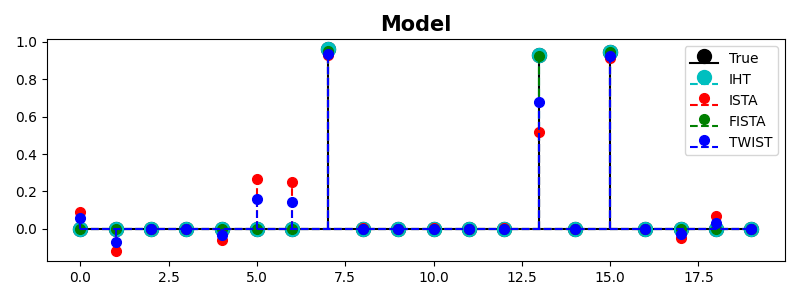
fig, ax = plt.subplots(1, 1, figsize=(8, 3))
m, s, b = ax.stem(x, linefmt='k', basefmt='k',
                  markerfmt='ko', label='True')
plt.setp(m, markersize=10)
m, s, b = ax.stem(x_iht, linefmt='--c', basefmt='--c',
                  markerfmt='co', label='IHT')
plt.setp(m, markersize=10)
m, s, b = ax.stem(x_ista, linefmt='--r', basefmt='--r',
                  markerfmt='ro', label='ISTA')
plt.setp(m, markersize=7)
m, s, b = ax.stem(x_fista, linefmt='--g', basefmt='--g',
                  markerfmt='go', label='FISTA')
plt.setp(m, markersize=7)
m, s, b = ax.stem(x_ander, linefmt='--m', basefmt='--m',
                  markerfmt='mo', label='AA-ISTA')
plt.setp(m, markersize=7)
m, s, b = ax.stem(x_twist, linefmt='--b', basefmt='--b',
                  markerfmt='bo', label='TWIST')
plt.setp(m, markersize=7)
ax.set_title('Model', size=15, fontweight='bold')
ax.legend()
plt.tight_layout()

Finally, let’s compare the converge behaviour of the different algorithms

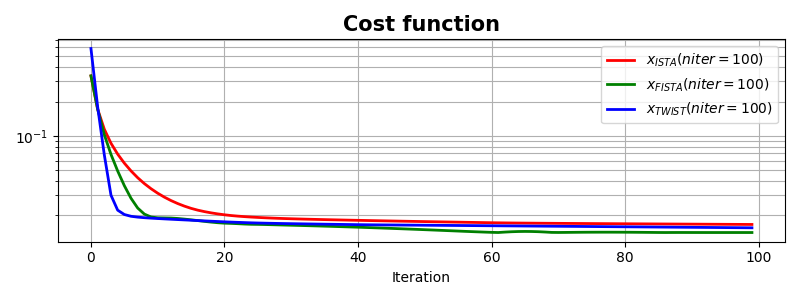
fig, ax = plt.subplots(1, 1, figsize=(8, 4))
ax.loglog(costi, 'r', lw=2, label=r'$x_{ISTA} (niter=%d)$' % niteri)
ax.loglog(costf, 'g', lw=2, label=r'$x_{FISTA} (niter=%d)$' % niterf)
ax.loglog(costa, 'm', lw=2, label=r'$x_{AA-ISTA} (niter=%d)$' % nitera)
ax.loglog(costt, 'b', lw=2, label=r'$x_{TWIST} (niter=%d)$' % maxit)
ax.set_title('Cost function', size=15, fontweight='bold')
ax.set_xlabel('Iteration')
ax.legend()
ax.grid(True, which='both')
plt.tight_layout()

To conclude, given the nature of the problem (small number of non-zero coefficients), the IHT solver shows the fastest convergence - note that we do not display the cost function since this is a constrained problem. This is however greatly influenced by the fact that we assume exact knowledge of the number of non-zero coefficients. When this information is not available, IHT may become suboptimal. In this case the FISTA or AA-ISTA solvers should always be preferred (over ISTA) and TwIST represents an alternative worth checking.