Note
Go to the end to download the full example code
Adaptive Primal-Dual#
This tutorial compares the traditional Chambolle-Pock Primal-dual algorithm with the Adaptive Primal-Dual Hybrid Gradient of Goldstein and co-authors.
By adaptively changing the step size in the primal and the dual directions, this algorithm shows faster convergence, which is of great importance for some of the problems that the Primal-Dual algorithm can solve - especially those with an expensive proximal operator.
For this example, we consider a simple denoising problem.
import numpy as np
import matplotlib.pyplot as plt
import pylops
from skimage.data import camera
import pyproximal
plt.close('all')
def callback(x, f, g, K, cost, xtrue, err):
cost.append(f(x) + g(K.matvec(x)))
err.append(np.linalg.norm(x - xtrue))
Let’s start by loading a sample image and adding some noise
We can now define a pylops.Gradient operator as well as the
different proximal operators to be passed to our solvers
# Gradient operator
sampling = 1.
Gop = pylops.Gradient(dims=(ny, nx), sampling=sampling, edge=False,
kind='forward', dtype='float64')
L = 8. / sampling ** 2 # maxeig(Gop^H Gop)
# L2 data term
lamda = .04
l2 = pyproximal.L2(b=noise_img.ravel(), sigma=lamda)
# L1 regularization (isotropic TV)
l1iso = pyproximal.L21(ndim=2)
To start, we solve our denoising problem with the original Primal-Dual algorithm
# Primal-dual
tau = 0.95 / np.sqrt(L)
mu = 0.95 / np.sqrt(L)
cost_fixed = []
err_fixed = []
iml12_fixed = \
pyproximal.optimization.primaldual.PrimalDual(l2, l1iso, Gop,
tau=tau, mu=mu, theta=1.,
x0=np.zeros_like(img.ravel()),
gfirst=False, niter=300, show=True,
callback=lambda x: callback(x, l2, l1iso,
Gop, cost_fixed,
img.ravel(),
err_fixed))
iml12_fixed = iml12_fixed.reshape(img.shape)
Primal-dual: min_x f(Ax) + x^T z + g(x)
---------------------------------------------------------
Proximal operator (f): <class 'pyproximal.proximal.L2.L2'>
Proximal operator (g): <class 'pyproximal.proximal.L21.L21'>
Linear operator (A): <class 'pylops.basicoperators.gradient.Gradient'>
Additional vector (z): None
tau = 0.33587572106361 mu = 0.33587572106361
theta = 1.00 niter = 300
Itn x[0] f g z^x J = f + g + z^x
1 2.59605e+00 1.148e+08 1.334e+05 0.000e+00 1.149e+08
2 5.16785e+00 1.118e+08 1.387e+05 0.000e+00 1.120e+08
3 7.70666e+00 1.090e+08 1.219e+05 0.000e+00 1.091e+08
4 1.01947e+01 1.062e+08 1.116e+05 0.000e+00 1.063e+08
5 1.26277e+01 1.035e+08 1.109e+05 0.000e+00 1.036e+08
6 1.50206e+01 1.008e+08 1.142e+05 0.000e+00 1.009e+08
7 1.73989e+01 9.824e+07 1.187e+05 0.000e+00 9.836e+07
8 1.97851e+01 9.573e+07 1.240e+05 0.000e+00 9.585e+07
9 2.21893e+01 9.327e+07 1.303e+05 0.000e+00 9.341e+07
10 2.46073e+01 9.089e+07 1.373e+05 0.000e+00 9.103e+07
31 6.73083e+01 5.302e+07 2.877e+05 0.000e+00 5.331e+07
61 1.11401e+02 2.521e+07 4.535e+05 0.000e+00 2.566e+07
91 1.40663e+02 1.268e+07 5.666e+05 0.000e+00 1.325e+07
121 1.60374e+02 7.032e+06 6.425e+05 0.000e+00 7.675e+06
151 1.73405e+02 4.479e+06 6.934e+05 0.000e+00 5.172e+06
181 1.82280e+02 3.321e+06 7.276e+05 0.000e+00 4.049e+06
211 1.88176e+02 2.794e+06 7.504e+05 0.000e+00 3.544e+06
241 1.92130e+02 2.552e+06 7.658e+05 0.000e+00 3.318e+06
271 1.94768e+02 2.440e+06 7.761e+05 0.000e+00 3.216e+06
292 1.96083e+02 2.399e+06 7.812e+05 0.000e+00 3.180e+06
293 1.96136e+02 2.398e+06 7.814e+05 0.000e+00 3.179e+06
294 1.96190e+02 2.396e+06 7.816e+05 0.000e+00 3.178e+06
295 1.96242e+02 2.395e+06 7.818e+05 0.000e+00 3.177e+06
296 1.96294e+02 2.394e+06 7.820e+05 0.000e+00 3.176e+06
297 1.96345e+02 2.392e+06 7.822e+05 0.000e+00 3.174e+06
298 1.96395e+02 2.391e+06 7.824e+05 0.000e+00 3.173e+06
299 1.96444e+02 2.390e+06 7.826e+05 0.000e+00 3.172e+06
300 1.96493e+02 2.388e+06 7.828e+05 0.000e+00 3.171e+06
Total time (s) = 11.12
---------------------------------------------------------
We do the same with the adaptive algorithm
cost_ada = []
err_ada = []
iml12_ada, steps = \
pyproximal.optimization.primaldual.AdaptivePrimalDual(l2, l1iso, Gop,
tau=tau, mu=mu,
x0=np.zeros_like(img.ravel()),
niter=45, show=True, tol=0.05,
callback=lambda x: callback(x, l2, l1iso,
Gop, cost_ada,
img.ravel(),
err_ada))
iml12_ada = iml12_ada.reshape(img.shape)
Adaptive Primal-dual: min_x f(Ax) + x^T z + g(x)
---------------------------------------------------------
Proximal operator (f): <class 'pyproximal.proximal.L2.L2'>
Proximal operator (g): <class 'pyproximal.proximal.L21.L21'>
Linear operator (A): <class 'pylops.basicoperators.gradient.Gradient'>
Additional vector (z): None
tau0 = 3.358757e-01 mu0 = 3.358757e-01
alpha0 = 5.000000e-01 eta = 9.500000e-01
s = 1.000000e+00 delta = 1.500000e+00
niter = 45 tol = 5.000000e-02
Itn x[0] f g z^x J = f + g + z^x
2 2.59605e+00 1.148e+08 1.334e+05 0.000e+00 1.149e+08
3 7.67236e+00 1.090e+08 1.628e+05 0.000e+00 1.092e+08
4 1.68656e+01 9.888e+07 2.031e+05 0.000e+00 9.909e+07
5 3.20891e+01 8.316e+07 2.856e+05 0.000e+00 8.345e+07
6 5.48988e+01 6.213e+07 4.068e+05 0.000e+00 6.253e+07
7 8.51166e+01 3.916e+07 5.550e+05 0.000e+00 3.971e+07
8 1.08951e+02 2.502e+07 6.633e+05 0.000e+00 2.568e+07
9 1.27808e+02 1.632e+07 7.381e+05 0.000e+00 1.705e+07
10 1.42763e+02 1.095e+07 7.890e+05 0.000e+00 1.174e+07
13 1.69078e+02 4.741e+06 8.547e+05 0.000e+00 5.596e+06
17 1.76349e+02 3.769e+06 8.439e+05 0.000e+00 4.613e+06
21 1.81309e+02 3.318e+06 8.310e+05 0.000e+00 4.149e+06
25 1.86364e+02 2.942e+06 8.410e+05 0.000e+00 3.783e+06
29 1.89516e+02 2.706e+06 8.327e+05 0.000e+00 3.539e+06
33 1.91169e+02 2.566e+06 8.158e+05 0.000e+00 3.382e+06
37 1.92282e+02 2.480e+06 8.052e+05 0.000e+00 3.286e+06
38 1.92568e+02 2.464e+06 8.035e+05 0.000e+00 3.268e+06
39 1.92870e+02 2.450e+06 8.023e+05 0.000e+00 3.253e+06
40 1.93192e+02 2.438e+06 8.013e+05 0.000e+00 3.239e+06
41 1.93531e+02 2.427e+06 8.005e+05 0.000e+00 3.227e+06
42 1.93886e+02 2.417e+06 7.999e+05 0.000e+00 3.217e+06
43 1.94253e+02 2.408e+06 7.995e+05 0.000e+00 3.208e+06
44 1.94625e+02 2.401e+06 7.991e+05 0.000e+00 3.200e+06
45 1.94997e+02 2.394e+06 7.988e+05 0.000e+00 3.193e+06
46 1.95363e+02 2.388e+06 7.986e+05 0.000e+00 3.186e+06
Total time (s) = 2.02
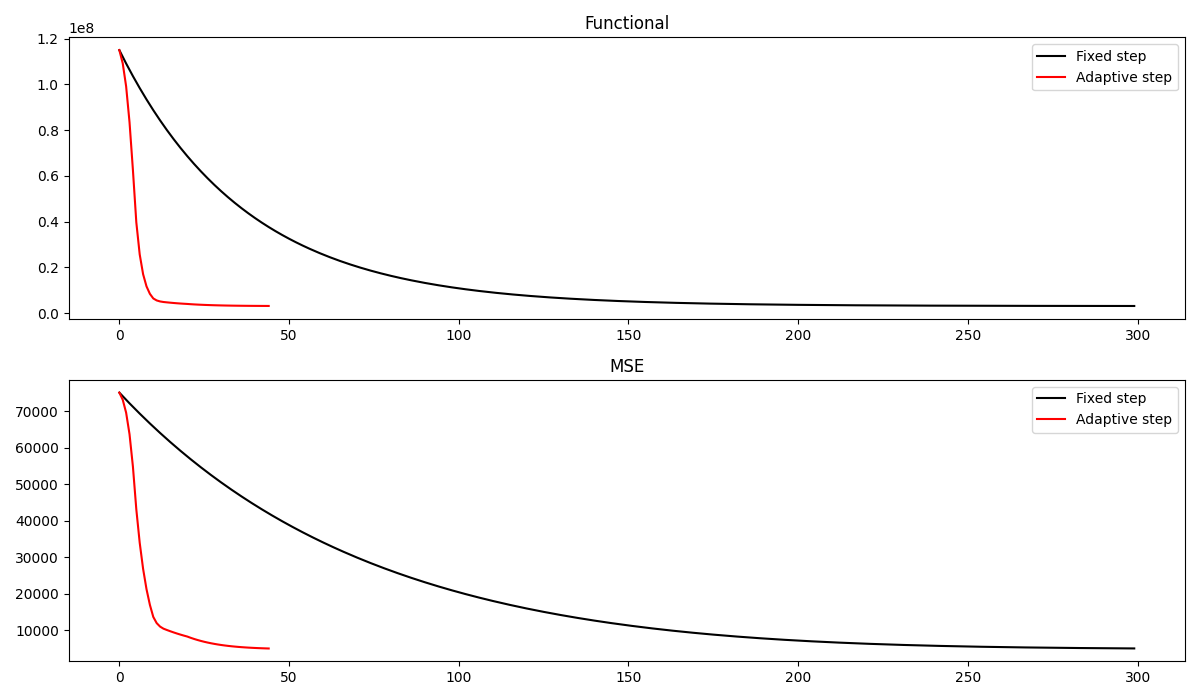
Let’s now compare the final results as well as the convergence curves of the two algorithms. We can see how the adaptive Primal-Dual produces a better estimate of the clean image in a much smaller number of iterations
fig, axs = plt.subplots(1, 4, figsize=(16, 4))
axs[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axs[0].set_title('Original')
axs[0].axis('off')
axs[0].axis('tight')
axs[1].imshow(noise_img, cmap='gray', vmin=0, vmax=255)
axs[1].set_title('Noisy')
axs[1].axis('off')
axs[1].axis('tight')
axs[2].imshow(iml12_fixed, cmap='gray', vmin=0, vmax=255)
axs[2].set_title('PD')
axs[2].axis('off')
axs[2].axis('tight')
axs[3].imshow(iml12_ada, cmap='gray', vmin=0, vmax=255)
axs[3].set_title('Adaptive PD')
axs[3].axis('off')
axs[3].axis('tight')
fig, axs = plt.subplots(2, 1, figsize=(12, 7))
axs[0].plot(cost_fixed, 'k', label='Fixed step')
axs[0].plot(cost_ada, 'r', label='Adaptive step')
axs[0].legend()
axs[0].set_title('Functional')
axs[1].plot(err_fixed, 'k', label='Fixed step')
axs[1].plot(err_ada, 'r', label='Adaptive step')
axs[1].set_title('MSE')
axs[1].legend()
plt.tight_layout()
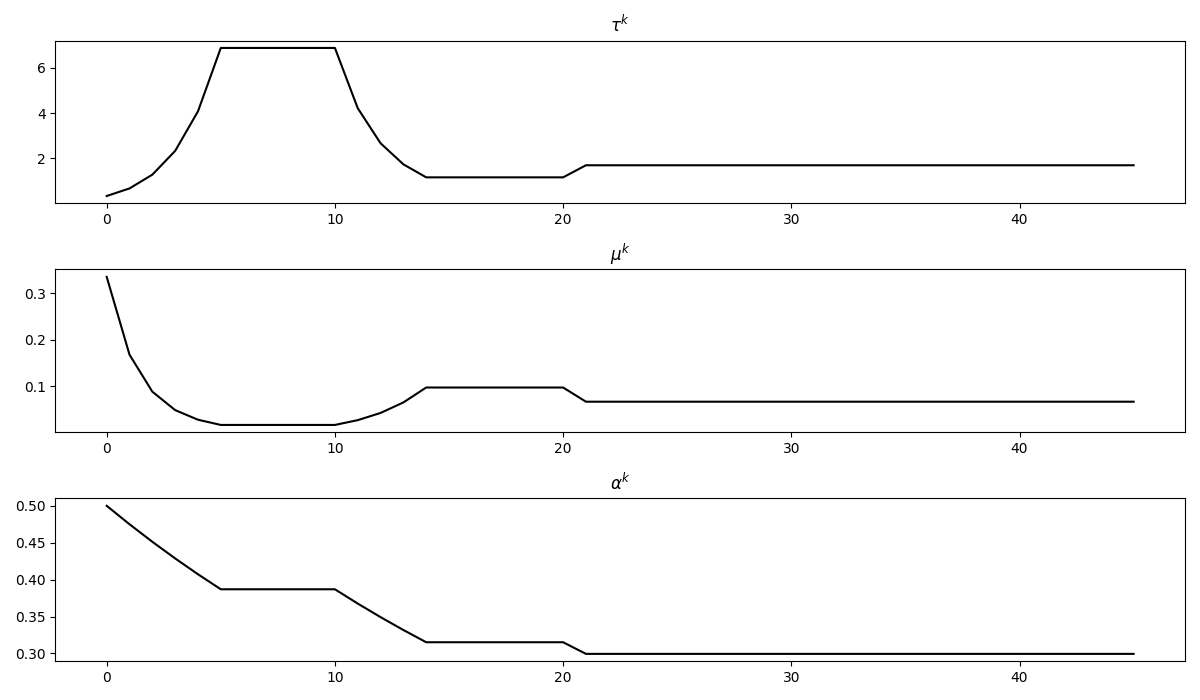
fig, axs = plt.subplots(3, 1, figsize=(12, 7))
axs[0].plot(steps[0], 'k')
axs[0].set_title(r'$\tau^k$')
axs[1].plot(steps[1], 'k')
axs[1].set_title(r'$\mu^k$')
axs[2].plot(steps[2], 'k')
axs[2].set_title(r'$\alpha^k$')
plt.tight_layout();
Total running time of the script: (0 minutes 14.230 seconds)