Note
Go to the end to download the full example code
Low-Rank completion via SVD#
In this tutorial we will present an example of low-rank matrix completion. Contrarily to most of the examples in this library (and PyLops), the regularizer is here applied to a matrix, which is obtained by reshaping the model vector that we wish to solve for.
In this example we will consider the following forward problem:
where \(\mathbf{R}\) is a restriction operator, which applied to \(\mathbf{x}=\operatorname{vec}(\mathbf{X})\), the vectorized version of a 2d image of size \(n \times m\), selects a reasonably small number of samples \(p \ll nm\) that form the vector \(\mathbf{y}\). Note that any other modelling operator could be used here, for example a 2D convolutional operator in the case of deblurring or a 2D FFT plus restriction in the case of MRI scanning.
The problem we want to solve can be mathematically described as:
or
where \(\|\mathbf{X}\|_*=\sum_i \sigma_i\) is the nuclear norm of \(\mathbf{X}\) (i.e., the sum of the singular values).
# sphinx_gallery_thumbnail_number = 2
import numpy as np
import matplotlib.pyplot as plt
import pylops
import pyproximal
from scipy import misc
np.random.seed(0)
plt.close('all')
Let’s start by loading a sample image
/home/docs/checkouts/readthedocs.org/user_builds/pyproximal/checkouts/stable/tutorials/lowrankcompletion.py:52: DeprecationWarning: scipy.misc.ascent has been deprecated in SciPy v1.10.0; and will be completely removed in SciPy v1.12.0. Dataset methods have moved into the scipy.datasets module. Use scipy.datasets.ascent instead.
X = misc.ascent()
We can now define a pylops.Restriction operator and look at how
the singular values of our image change when we remove some of its sample.
# Restriction operator
sub = 0.4
nsub = int(ny*nx*sub)
iava = np.random.permutation(np.arange(ny*nx))[:nsub]
Rop = pylops.Restriction(ny*nx, iava)
# Data
y = Rop * X.ravel()
# Masked data
Y = (Rop.H * Rop * X.ravel()).reshape(ny, nx)
# SVD of true and masked data
Ux, Sx, Vhx = np.linalg.svd(X, full_matrices=False)
Uy, Sy, Vhy = np.linalg.svd(Y, full_matrices=False)
plt.figure()
plt.semilogy(Sx, 'k', label=r'$||X||_*$=%.2f' % np.sum(Sx))
plt.semilogy(Sy, 'r', label=r'$||Y||_*$=%.2f' % np.sum(Sy))
plt.legend()
plt.tight_layout()
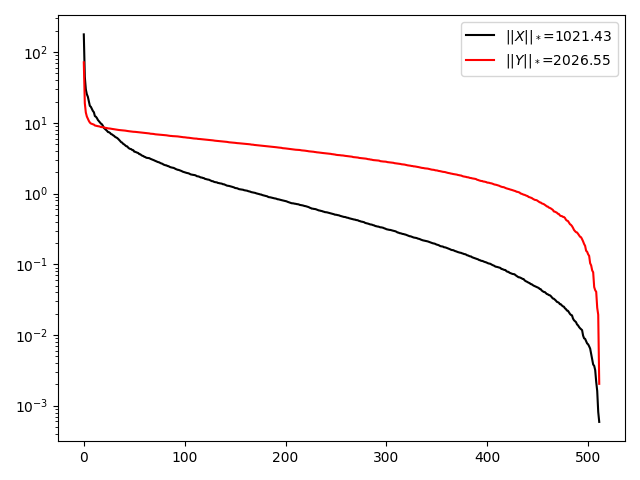
We observe that removing some samples from the image has led to an overall increase in the singular values of \(\mathbf{X}\), especially those that are originally very small. As a consequence the nuclear norm of \(\mathbf{Y}\) (the masked image) is larger than that of \(\mathbf{X}\).
Let’s now set up the inverse problem using the Proximal gradient algorithm
mu = .8
f = pyproximal.L2(Rop, y)
g = pyproximal.Nuclear((ny, nx), mu)
Xpg = pyproximal.optimization.primal.ProximalGradient(f, g, np.zeros(ny*nx), acceleration='vandenberghe',
tau=1., niter=100, show=True)
Xpg = Xpg.reshape(ny, nx)
# Recompute SVD and see how the singular values look like
Upg, Spg, Vhpg = np.linalg.svd(Xpg, full_matrices=False)
Accelerated Proximal Gradient
---------------------------------------------------------
Proximal operator (f): <class 'pyproximal.proximal.L2.L2'>
Proximal operator (g): <class 'pyproximal.proximal.Nuclear.Nuclear'>
tau = 1.0 beta=5.000000e-01
epsg = 1.0 niter = 100
niterback = 100 acceleration = vandenberghe
Itn x[0] f g J=f+eps*g tau
1 2.80234e-01 9.762e+01 1.314e+03 1.412e+03 1.000e+00
2 2.79868e-01 9.629e+01 1.223e+03 1.319e+03 1.000e+00
3 2.89674e-01 9.359e+01 1.129e+03 1.222e+03 1.000e+00
4 2.94030e-01 9.019e+01 1.035e+03 1.125e+03 1.000e+00
5 3.00071e-01 8.645e+01 9.438e+02 1.030e+03 1.000e+00
6 3.07346e-01 8.300e+01 8.565e+02 9.395e+02 1.000e+00
7 3.16868e-01 8.025e+01 7.742e+02 8.545e+02 1.000e+00
8 3.16858e-01 7.828e+01 6.988e+02 7.770e+02 1.000e+00
9 3.13267e-01 7.674e+01 6.331e+02 7.098e+02 1.000e+00
10 3.13406e-01 7.566e+01 5.796e+02 6.553e+02 1.000e+00
11 3.14952e-01 7.515e+01 5.400e+02 6.151e+02 1.000e+00
21 3.06372e-01 7.479e+01 4.884e+02 5.631e+02 1.000e+00
31 3.12195e-01 7.520e+01 4.869e+02 5.621e+02 1.000e+00
41 3.11005e-01 7.515e+01 4.868e+02 5.620e+02 1.000e+00
51 3.11186e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
61 3.11239e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
71 3.11139e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
81 3.11222e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
91 3.11167e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
92 3.11171e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
93 3.11176e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
94 3.11181e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
95 3.11186e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
96 3.11191e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
97 3.11194e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
98 3.11197e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
99 3.11199e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
100 3.11199e-01 7.518e+01 4.868e+02 5.620e+02 1.000e+00
Total time (s) = 12.12
---------------------------------------------------------
Let’s do the same with the constrained version
mu1 = 0.8 * np.sum(Sx)
g = pyproximal.proximal.NuclearBall((ny, nx), mu1)
Xpgc = pyproximal.optimization.primal.ProximalGradient(f, g, np.zeros(ny*nx), acceleration='vandenberghe',
tau=1., niter=100, show=True)
Xpgc = Xpgc.reshape(ny, nx)
# Recompute SVD and see how the singular values look like
Upgc, Spgc, Vhpgc = np.linalg.svd(Xpgc, full_matrices=False)
Accelerated Proximal Gradient
---------------------------------------------------------
Proximal operator (f): <class 'pyproximal.proximal.L2.L2'>
Proximal operator (g): <class 'pyproximal.proximal.Nuclear.NuclearBall'>
tau = 1.0 beta=5.000000e-01
epsg = 1.0 niter = 100
niterback = 100 acceleration = vandenberghe
Itn x[0] f g J=f+eps*g tau
1 1.90702e-01 1.162e+03 0.000e+00 1.162e+03 1.000e+00
2 2.53265e-01 6.432e+02 0.000e+00 6.432e+02 1.000e+00
3 2.86505e-01 3.437e+02 1.000e+00 3.447e+02 1.000e+00
4 3.04911e-01 1.802e+02 0.000e+00 1.802e+02 1.000e+00
5 3.12726e-01 9.470e+01 1.000e+00 9.570e+01 1.000e+00
6 3.15842e-01 5.078e+01 1.000e+00 5.178e+01 1.000e+00
7 3.17937e-01 2.813e+01 0.000e+00 2.813e+01 1.000e+00
8 3.18902e-01 1.623e+01 1.000e+00 1.723e+01 1.000e+00
9 3.18828e-01 9.769e+00 0.000e+00 9.769e+00 1.000e+00
10 3.19034e-01 6.129e+00 0.000e+00 6.129e+00 1.000e+00
11 3.19980e-01 3.995e+00 1.000e+00 4.995e+00 1.000e+00
21 3.25186e-01 1.995e-01 0.000e+00 1.995e-01 1.000e+00
31 3.25431e-01 2.777e-02 1.000e+00 1.028e+00 1.000e+00
41 3.25451e-01 4.893e-03 1.000e+00 1.005e+00 1.000e+00
51 3.25465e-01 7.274e-04 0.000e+00 7.274e-04 1.000e+00
61 3.25484e-01 4.032e-05 0.000e+00 4.032e-05 1.000e+00
71 3.25491e-01 7.626e-09 1.000e+00 1.000e+00 1.000e+00
81 3.25490e-01 9.189e-09 0.000e+00 9.189e-09 1.000e+00
91 3.25490e-01 1.053e-08 0.000e+00 1.053e-08 1.000e+00
92 3.25491e-01 9.221e-08 1.000e+00 1.000e+00 1.000e+00
93 3.25490e-01 1.089e-08 0.000e+00 1.089e-08 1.000e+00
94 3.25490e-01 1.074e-08 0.000e+00 1.074e-08 1.000e+00
95 3.25490e-01 1.064e-08 0.000e+00 1.064e-08 1.000e+00
96 3.25490e-01 1.061e-08 0.000e+00 1.061e-08 1.000e+00
97 3.25490e-01 1.061e-08 0.000e+00 1.061e-08 1.000e+00
98 3.25490e-01 1.062e-08 0.000e+00 1.062e-08 1.000e+00
99 3.25490e-01 1.064e-08 0.000e+00 1.064e-08 1.000e+00
100 3.25490e-01 1.066e-08 0.000e+00 1.066e-08 1.000e+00
Total time (s) = 13.29
---------------------------------------------------------
And finally we display the reconstructed image
plt.figure()
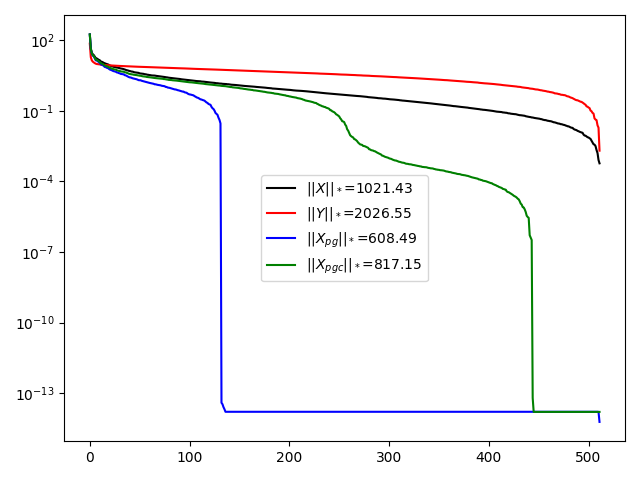
plt.semilogy(Sx, 'k', label=r'$||X||_*$=%.2f' % np.sum(Sx))
plt.semilogy(Sy, 'r', label=r'$||Y||_*$=%.2f' % np.sum(Sy))
plt.semilogy(Spg, 'b', label=r'$||X_{pg}||_*$=%.2f' % np.sum(Spg))
plt.semilogy(Spgc, 'g', label=r'$||X_{pgc}||_*$=%.2f' % np.sum(Spgc))
plt.legend()
plt.tight_layout()
fig, axs = plt.subplots(1, 4, figsize=(14, 6))
axs[0].imshow(X, cmap='gray')
axs[0].set_title('True')
axs[1].imshow(Y, cmap='gray')
axs[1].set_title('Masked')
axs[2].imshow(Xpg, cmap='gray')
axs[2].set_title('Reconstructed reg.')
axs[3].imshow(Xpgc, cmap='gray')
axs[3].set_title('Reconstructed constr.')
fig.tight_layout()
Total running time of the script: (0 minutes 27.185 seconds)