pyproximal.L2#
- class pyproximal.L2(Op=None, b=None, q=None, sigma=1.0, alpha=1.0, qgrad=True, niter=10, x0=None, warm=True, densesolver=None, kwargs_solver=None)[source]#
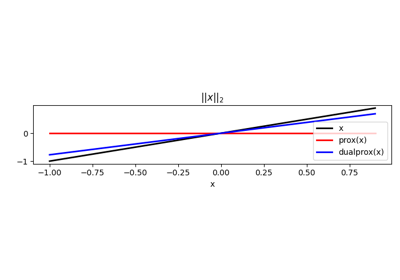
L2 Norm proximal operator.
The Proximal operator of the \(\ell_2\) norm is defined as: \(f(\mathbf{x}) = \frac{\sigma}{2} ||\mathbf{Op}\mathbf{x} - \mathbf{b}||_2^2\) and \(f_\alpha(\mathbf{x}) = f(\mathbf{x}) + \alpha \mathbf{q}^T\mathbf{x}\).
- Parameters
- Op
pylops.LinearOperator, optional Linear operator
- b
numpy.ndarray, optional Data vector
- q
numpy.ndarray, optional Dot vector
- sigma
int, optional Multiplicative coefficient of L2 norm
- alpha
float, optional Multiplicative coefficient of dot product
- qgrad
bool, optional Add q term to gradient (
True) or not (False)- niter
intorfunc, optional Number of iterations of iterative scheme used to compute the proximal. This can be a constant number or a function that is called passing a counter which keeps track of how many times the
proxmethod has been invoked before and returns theniterto be used.- x0
np.ndarray, optional Initial vector
- warm
bool, optional Warm start (
True) or not (False). Uses estimate from previous call ofproxmethod.- densesolver
str, optional Use
numpy,scipy, orfactorizewhen dealing with explicit operators. The former two rely on dense solvers from either library, whilst the last computes a factorization of the matrix to invert and avoids to do so unless the \(\tau\) or \(\sigma\) paramets have changed. Choosedensesolver=Nonewhen using PyLops versions earlier than v1.18.1 or v2.0.0- **kwargs_solver
dict, optional Dictionary containing extra arguments for
scipy.sparse.linalg.lsqrsolver when using numpy data (orpylops.optimization.solver.lsqrand when using cupy data)
- Op
Notes
The L2 proximal operator is defined as:
\[prox_{\tau f_\alpha}(\mathbf{x}) = \left(\mathbf{I} + \tau \sigma \mathbf{Op}^T \mathbf{Op} \right)^{-1} \left( \mathbf{x} + \tau \sigma \mathbf{Op}^T \mathbf{b} - \tau \alpha \mathbf{q}\right)\]when both
Opandbare provided. This formula shows that the proximal operator requires the solution of an inverse problem. If the operatorOpis of kindexplicit=True, we can solve this problem directly. On the other hand ifOpis of kindexplicit=False, an iterative solver is employed. In this case it is possible to provide a warm start via thex0input parameter.When only
bis provided,Opis assumed to be an Identity operator and the proximal operator reduces to:\[\prox_{\tau f_\alpha}(\mathbf{x}) = \frac{\mathbf{x} + \tau \sigma \mathbf{b} - \tau \alpha \mathbf{q}} {1 + \tau \sigma}\]If
bis not provided, the proximal operator reduces to:\[\prox_{\tau f_\alpha}(\mathbf{x}) = \frac{\mathbf{x} - \tau \alpha \mathbf{q}}{1 + \tau \sigma}\]Finally, note that the second term in \(f_\alpha(\mathbf{x})\) is added because this combined expression appears in several problems where Bregman iterations are used alongside a proximal solver.
Methods
__init__([Op, b, q, sigma, alpha, qgrad, ...])affine_addition(v)Affine addition
chain(g)Chain
grad(x)Compute gradient
postcomposition(sigma)Postcomposition
precomposition(a, b)Precomposition
prox(*args, **kwargs)proxdual(**kwargs)
Examples using pyproximal.L2#
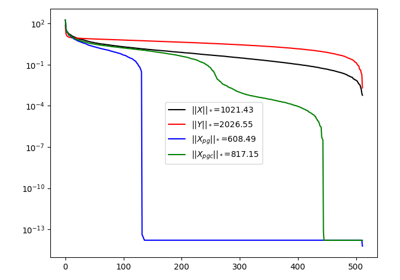
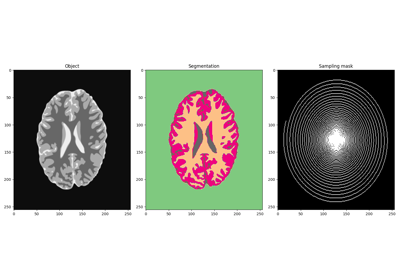
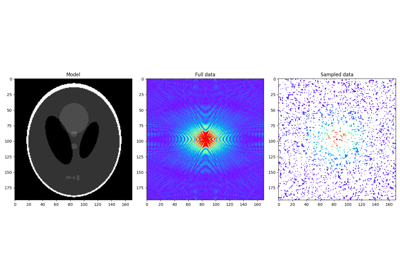
IHT, ISTA, FISTA, and TWIST for Compressive sensing