Note
Go to the end to download the full example code
Norms#
This example shows how to compute proximal operators of different norms, namely:
Euclidean norm (
pyproximal.Euclidean)L2 norm (
pyproximal.L2)L1 norm (
pyproximal.L1)L21 norm (
pyproximal.L21)
import numpy as np
import matplotlib.pyplot as plt
import pylops
import pyproximal
plt.close('all')
Let’s start with the Euclidean norm. We define a vector \(\mathbf{x}\) and a scalar \(\sigma\) and compute the norm. We then define the proximal scalar \(\tau\) and compute the proximal operator and its dual.
eucl = pyproximal.Euclidean(sigma=2.)
x = np.arange(-1, 1, 0.1)
print('||x||_2: ', eucl(x))
tau = 2
xp = eucl.prox(x, tau)
xdp = eucl.proxdual(x, tau)
plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.plot(x, xdp, 'b', lw=2, label='dualprox(x)')
plt.xlabel('x')
plt.title(r'$||x||_2$')
plt.legend()
plt.tight_layout()
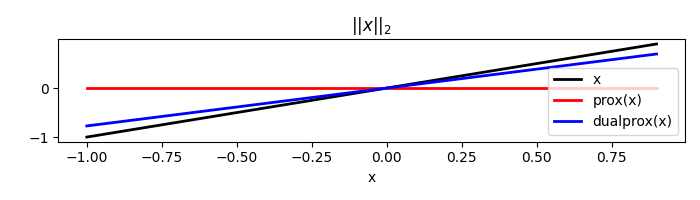
||x||_2: 5.176871642217913
Similarly we can do the same for the L2 norm (i.e., square of Euclidean norm)
l2 = pyproximal.L2(sigma=2.)
x = np.arange(-1, 1, 0.1)
print('||x||_2^2: ', l2(x))
tau = 2
xp = l2.prox(x, tau)
xdp = l2.proxdual(x, tau)
plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.plot(x, xdp, 'b', lw=2, label='dualprox(x)')
plt.xlabel('x')
plt.title(r'$||x||_2^2$')
plt.legend()
plt.tight_layout()
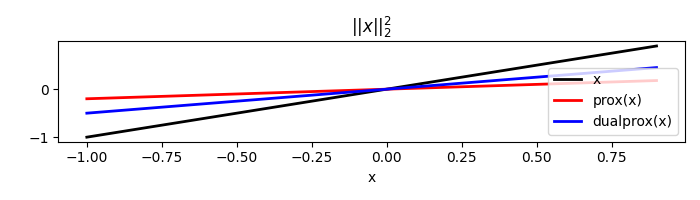
||x||_2^2: 6.6999999999999975
For this norm we can also subtract a vector to x and multiply x by a matrix A
l2 = pyproximal.L2(sigma=2., b=np.ones_like(x))
x = np.arange(-1, 1, 0.1)
print('||x-b||_2^2: ', l2(x))
tau = 2
xp = l2.prox(x, tau)
xdp = l2.proxdual(x, tau)
plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.plot(x, xdp, 'b', lw=2, label='dualprox(x)')
plt.xlabel('x')
plt.title(r'$||x-b||_2^2$')
plt.legend()
plt.tight_layout()
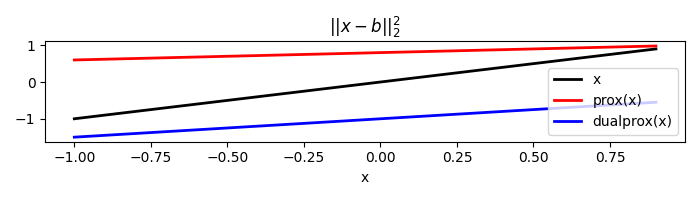
||x-b||_2^2: 28.70000000000001
Finally we can also multiply x by a matrix A
x = np.arange(-1, 1, 0.1)
nx = len(x)
ny = nx * 2
A = np.random.normal(0, 1, (ny, nx))
l2 = pyproximal.L2(sigma=2.,b=np.ones(ny), Op=pylops.MatrixMult(A))
print('||Ax-b||_2^2: ', l2(x))
tau = 2
xp = l2.prox(x, tau)
xdp = l2.proxdual(x, tau)
plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.plot(x, xdp, 'b', lw=2, label='dualprox(x)')
plt.xlabel('x')
plt.title(r'$||Ax-b||_2^2$')
plt.legend()
plt.tight_layout()
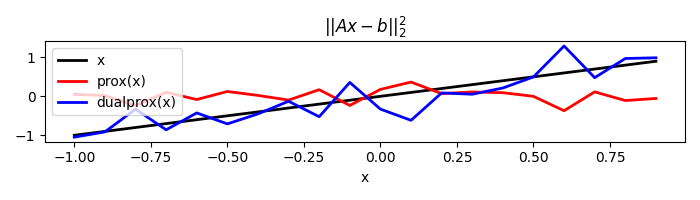
||Ax-b||_2^2: 192.95529752102033
We consider now the L1 norm. Here the proximal operator can be easily computed using the so-called soft-thresholding operation on each element of the input vector
l1 = pyproximal.L1(sigma=1.)
x = np.arange(-1, 1, 0.1)
print('||x||_1: ', l1(x))
tau = 0.5
xp = l1.prox(x, tau)
xdp = l1.proxdual(x, tau)
plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.plot(x, xdp, 'b', lw=2, label='dualprox(x)')
plt.xlabel('x')
plt.title(r'$||x||_1$')
plt.legend()
plt.tight_layout()
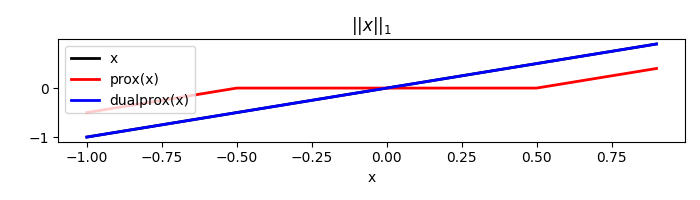
||x||_1: 9.999999999999996
We consider now the TV norm.
TV = pyproximal.TV(dims=(nx, ), sigma=1.)
x = np.arange(-1, 1, 0.1)
print('||x||_{TV}: ', l1(x))
tau = 0.5
xp = TV.prox(x, tau)
plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.xlabel('x')
plt.title(r'$||x||_{TV}$')
plt.legend()
plt.tight_layout()
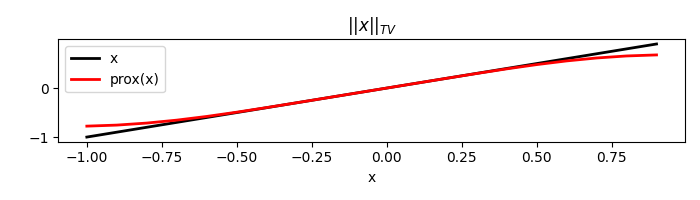
||x||_{TV}: 9.999999999999996
Total running time of the script: (0 minutes 1.211 seconds)
