pyproximal.ETP

class pyproximal.ETP(sigma, gamma=1.0)

Exponential-type penalty (ETP).

The exponential-type penalty is defined as

\[\mathrm{ETP}_{\sigma,\gamma}(\mathbf{x}) = \sum_i \frac{\sigma}{1-e^{-\gamma}}(1-e^{-\gamma|x_i|})\]

for \({\sigma>0}\), and \({\gamma>0}\).

Parameters

sigmafloat

Regularization parameter.

gammafloat, optional

Regularization parameter. Default is 1.0.

Notes

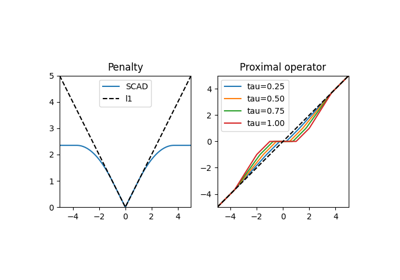
As \({\gamma\rightarrow 0}\) the exponential-type penalty approaches the \(\ell_1\)-penalty and when \({\gamma\rightarrow\infty}\) tends to the \(\ell_0\)-penalty [1].

As for the proximal operator, consider the one-dimensional case

\[\prox_{\tau \mathrm{ETP}(\cdot)}(x) = \argmin_{z} \mathrm{ETP}(z) + \frac{1}{2\tau}(x - z)^2\]

and assume that \(x\geq 0\). The minima can be obtained when \(z=0\) or at a stationary point, where the latter must satisfy

\[x = z + \frac{\gamma \sigma \tau}{1-e^{-\gamma}} e^{-\gamma z} .\]

The solution to the above equation can be expressed using the Lambert W function.

1

Gao, C. et al. “A Feasible Nonconvex Relaxation Approach to Feature Selection”, In the Proceedings of the Conference on Artificial Intelligence (AAAI), 2011.

Methods

__init__(sigma[, gamma])
affine_addition(v)	Affine addition
chain(g)	Chain
elementwise(x)
grad(x)	Compute gradient
postcomposition(sigma)	Postcomposition
precomposition(a, b)	Precomposition
prox(**kwargs)
proxdual(**kwargs)

Examples using pyproximal.ETP

Concave penalties

Concave penalties