pyproximal.ProxOperator#
- class pyproximal.ProxOperator(Op=None, hasgrad=False)[source]#
Common interface for proximal operators of a function.
This class defines the overarching structure of any proximal operator. It contains two main methods,
proxanddualproxwhich are both implemented by means of the Moreau decomposition assuming explicit knowledge of the other method. For this reason any proximal operators that subclasses theProxOperatorclass needs at least one of these two methods to be implemented directly.Note
End users of PyProx should not use this class directly but simply use operators that are already implemented. This class is meant for developers and it has to be used as the parent class of any new operator developed within PyProx. Find more details regarding implementation of new operators at Implementing new operators.
- Parameters
- Op
pylops.LinearOperator, optional Linear operator used by the Proximal operator
- hasgrad
bool, optional Flag to indicate if the function is differentiable, i.e., has a uniquely defined gradient (
True) or not (False).
- Op
Notes
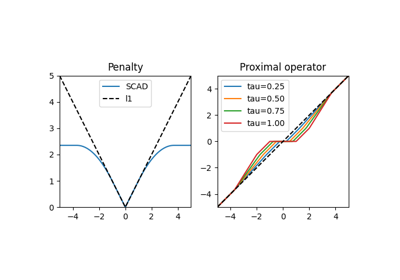
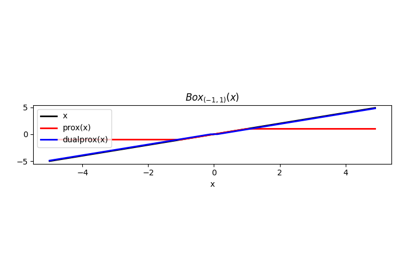
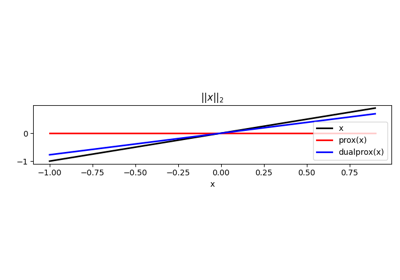
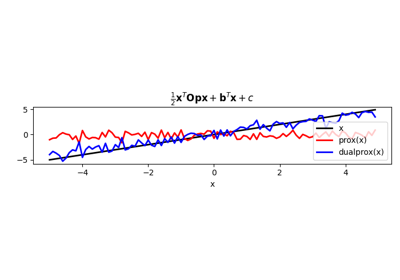
The proximal operator of a function
fis defined as:\[prox_{\tau f} (\mathbf{x}) = \argmin_{\mathbf{y}} f(\mathbf{y}) + \frac{1}{2 \tau}||\mathbf{y} - \mathbf{x}||^2_2\]Methods
__init__([Op, hasgrad])affine_addition(v)Affine addition
chain(g)Chain
grad(x)Compute gradient
postcomposition(sigma)Postcomposition
precomposition(a, b)Precomposition
prox(**kwargs)proxdual(**kwargs)
Examples using pyproximal.ProxOperator#
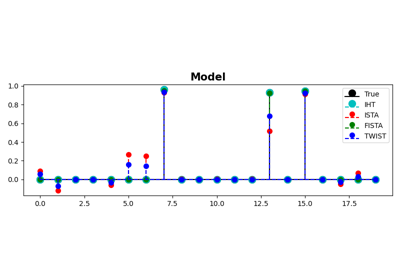
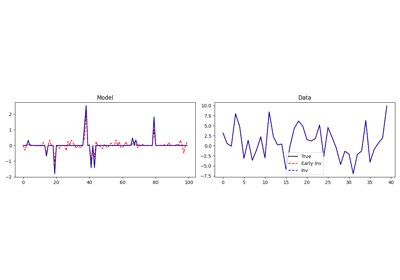
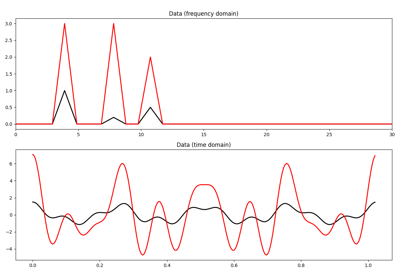
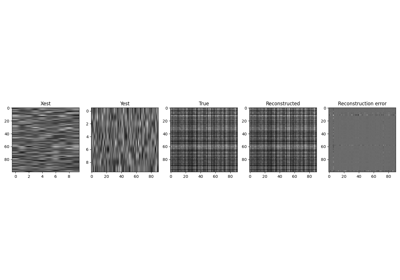
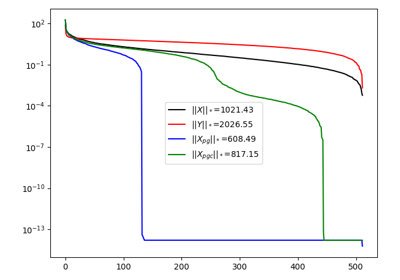
IHT, ISTA, FISTA, and TWIST for Compressive sensing