Norms

This example considers proximal operators of indicator functions, which can be computed via their orthogonal projections.

import numpy as np
import matplotlib.pyplot as plt
import pylops

import pyproximal

plt.close('all')

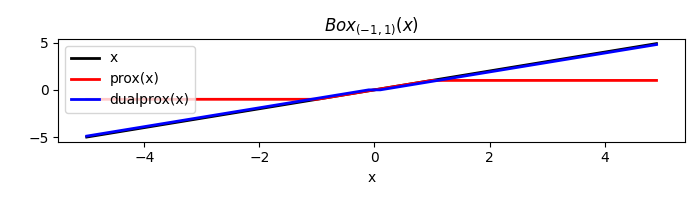
Let’s start with a Box. We can define its lower and upper bound (where either of them could be infinity (for a semi-bounded box).

box = pyproximal.Box(-1, 1)

x = np.arange(-5, 5, 0.1)
xc = box(x)
print('Box_(-1, 1)(x): ', box(x))

tau = 0.1
xp = box.prox(x, tau)
xdp = box.proxdual(x, tau)

plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.plot(x, xdp, 'b', lw=2, label='dualprox(x)')
plt.xlabel('x')
plt.title(r'$Box_{(-1, 1)}(x)$')
plt.legend()
plt.tight_layout()

Box_(-1, 1)(x):  0.0

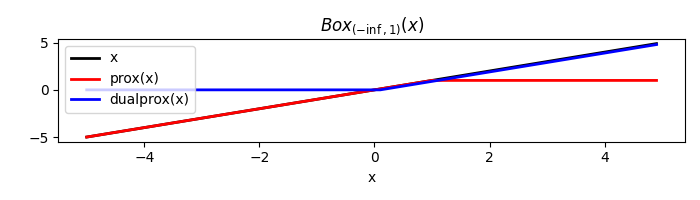
Similarly we can define only one of the two bounds, with the other set to infinity for a semi-bounded box.

box = pyproximal.Box(upper=1)

x = np.arange(-5, 5, 0.1)
xc = box(x)
print('Box_(-inf, 1)(x): ', box(x))

tau = 0.1
xp = box.prox(x, tau)
xdp = box.proxdual(x, tau)

plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.plot(x, xdp, 'b', lw=2, label='dualprox(x)')
plt.xlabel('x')
plt.title(r'$Box_{(-\inf, 1)}(x)$')
plt.legend()
plt.tight_layout()

Box_(-inf, 1)(x):  0.0

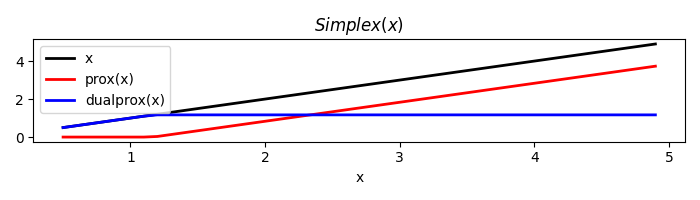
We now consider a Simplex. This proximal operator can be used every time we want to ensure that the sum of the coefficients of a vector is equal a certain number \(r\). called the radius. All the coefficients will also be forced to be positive.

x = np.arange(0.5, 5, 0.1)
nx = len(x)

sim = pyproximal.Simplex(n=nx, radius=np.sum(x) - 50)
print('Simplex(x): ', sim(x))

tau = 4
xp = sim.prox(x, 1)
xdp = sim.proxdual(x, 1)

plt.figure(figsize=(7, 2))
plt.plot(x, x, 'k', lw=2, label='x')
plt.plot(x, xp, 'r', lw=2, label='prox(x)')
plt.plot(x, xdp, 'b', lw=2, label='dualprox(x)')
plt.xlabel('x')
plt.title(r'$Simplex(x)$')
plt.legend()
plt.tight_layout()

Simplex(x):  False