Basis Pursuit

This tutorial considers the Basis Pursuit problem. From a mathematical point of view we seek the sparsest solution that satisfies a system of equations.

\[\argmin_\mathbf{x} \|\mathbf{x}\|_1 \; \text{s.t.} \; \mathbf{Ax} = \mathbf{y}\]

where the operator \(\mathbf{A}\) is of size \(N \times M\), and generally \(N<M\). Note that this problem is similar to more general L1-regularized inversion, but it presents a stricter condition on the data term which must be satisfied exactly. Similarly, we can also consider the Basis Pursuit Denoise problem

\[\argmin_\mathbf{x} \|\mathbf{x}\|_1 \; \text{s.t.} \; \|\mathbf{Ax} - \mathbf{y}\|_2 < \epsilon\]

import numpy as np
import matplotlib.pyplot as plt
import pylops
from scipy import misc

import pyproximal

plt.close('all')
np.random.seed(10)

Let’s start by creating the input vector x and operator A, and data y

n, m = 40, 100
mava = 10

# model
x = np.zeros(m)
iava = np.random.permutation(np.arange(m))[:mava]
x[iava] = np.random.normal(0, 1, mava)

# operator
A = np.random.normal(0, 1, (n, m))
Aop = pylops.MatrixMult(A)
Aop.explicit = False  # temporary solution whilst PyLops gets updated

y = Aop * x

This problem can be solved using the ADMM solver where f is an Affine set and g is the L1 norm

f = pyproximal.AffineSet(Aop, y, niter=20)
g = pyproximal.L1()

xinv_early = pyproximal.optimization.primal.ADMM(f, g, np.zeros_like(x),
                                                 0.1, niter=10, show=True)[0]

xinv = pyproximal.optimization.primal.ADMM(f, g, np.zeros_like(x),
                                           0.1, niter=150, show=True)[0]

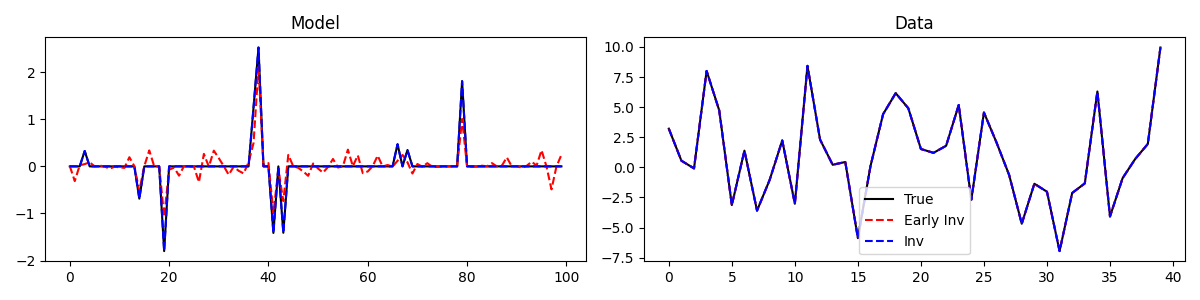
fig, axs = plt.subplots(1, 2, figsize=(12, 3))
axs[0].plot(x, 'k')
axs[0].plot(xinv_early, '--r')
axs[0].plot(xinv, '--b')
axs[0].set_title('Model')
axs[1].plot(y, 'k', label='True')
axs[1].plot(Aop * xinv_early, '--r', label='Early Inv')
axs[1].plot(Aop * xinv, '--b', label='Inv')
axs[1].set_title('Data')
axs[1].legend()
plt.tight_layout()

ADMM
---------------------------------------------------------
Proximal operator (f): <class 'pyproximal.proximal.AffineSet.AffineSet'>
Proximal operator (g): <class 'pyproximal.proximal.L1.L1'>
tau = 1.000000e-01      niter = 10

   Itn       x[0]          f           g       J = f + g
     1  -1.48208e-01   0.000e+00   1.979e+01   1.979e+01
     2  -1.17824e-01   0.000e+00   1.716e+01   1.716e+01
     3  -1.04548e-01   0.000e+00   1.667e+01   1.667e+01
     4  -7.88774e-02   0.000e+00   1.627e+01   1.627e+01
     5  -3.42487e-02   0.000e+00   1.598e+01   1.598e+01
     6   1.10090e-02   0.000e+00   1.558e+01   1.558e+01
     7   4.01171e-02   0.000e+00   1.531e+01   1.531e+01
     8   2.07255e-02   0.000e+00   1.520e+01   1.520e+01
     9   1.29133e-02   0.000e+00   1.496e+01   1.496e+01
    10   6.58063e-03   0.000e+00   1.463e+01   1.463e+01

Total time (s) = 0.01
---------------------------------------------------------

ADMM
---------------------------------------------------------
Proximal operator (f): <class 'pyproximal.proximal.AffineSet.AffineSet'>
Proximal operator (g): <class 'pyproximal.proximal.L1.L1'>
tau = 1.000000e-01      niter = 150

   Itn       x[0]          f           g       J = f + g
     1  -1.48208e-01   0.000e+00   1.979e+01   1.979e+01
     2  -1.17824e-01   0.000e+00   1.716e+01   1.716e+01
     3  -1.04548e-01   0.000e+00   1.667e+01   1.667e+01
     4  -7.88774e-02   0.000e+00   1.627e+01   1.627e+01
     5  -3.42487e-02   0.000e+00   1.598e+01   1.598e+01
     6   1.10090e-02   0.000e+00   1.558e+01   1.558e+01
     7   4.01171e-02   0.000e+00   1.531e+01   1.531e+01
     8   2.07255e-02   0.000e+00   1.520e+01   1.520e+01
     9   1.29133e-02   0.000e+00   1.496e+01   1.496e+01
    10   6.58063e-03   0.000e+00   1.463e+01   1.463e+01
    16  -1.66119e-03   0.000e+00   1.368e+01   1.368e+01
    31  -4.17020e-03   0.000e+00   1.250e+01   1.250e+01
    46   1.95677e-04   0.000e+00   1.209e+01   1.209e+01
    61   1.07793e-04   0.000e+00   1.205e+01   1.205e+01
    76   4.61062e-07   0.000e+00   1.204e+01   1.204e+01
    91   1.77417e-07   0.000e+00   1.204e+01   1.204e+01
   106   6.46170e-07   0.000e+00   1.203e+01   1.203e+01
   121   4.57747e-07   0.000e+00   1.203e+01   1.203e+01
   136   4.28310e-07   0.000e+00   1.203e+01   1.203e+01
   142   4.38472e-07   0.000e+00   1.203e+01   1.203e+01
   143   4.39766e-07   0.000e+00   1.203e+01   1.203e+01
   144   4.39837e-07   0.000e+00   1.203e+01   1.203e+01
   145   4.38918e-07   0.000e+00   1.203e+01   1.203e+01
   146   4.37419e-07   0.000e+00   1.203e+01   1.203e+01
   147   4.35799e-07   0.000e+00   1.203e+01   1.203e+01
   148   4.34448e-07   0.000e+00   1.203e+01   1.203e+01
   149   4.33615e-07   0.000e+00   1.203e+01   1.203e+01
   150   4.33383e-07   0.000e+00   1.203e+01   1.203e+01

Total time (s) = 0.14
---------------------------------------------------------

We can observe how even after few iterations, despite the solution is not yet converged the data reconstruction is perfect. This is consequence of the fact that for the Basis Pursuit problem the data term is a hard constraint. Finally let’s consider the case with a soft constraint.

f = pyproximal.L1()
g = pyproximal.proximal.EuclideanBall(y, .1)

L = np.real((Aop.H @ Aop).eigs(1))[0]
tau = .99
mu = tau / L

xinv_early = pyproximal.optimization.primaldual.PrimalDual(f, g, Aop, np.zeros_like(x),
                                                           tau, mu, niter=10)

xinv = pyproximal.optimization.primaldual.PrimalDual(f, g, Aop, np.zeros_like(x),
                                                     tau, mu, niter=1000)

fig, axs = plt.subplots(1, 2, figsize=(12, 3))
axs[0].plot(x, 'k')
axs[0].plot(xinv_early, '--r')
axs[0].plot(xinv, '--b')
axs[0].set_title('Model')
axs[1].plot(y, 'k', label='True')
axs[1].plot(Aop * xinv_early, '--r', label='Early Inv')
axs[1].plot(Aop * xinv, '--b', label='Inv (Res=%.2f)' % np.linalg.norm(y - Aop @ xinv))
axs[1].set_title('Data')
axs[1].legend()
plt.tight_layout()

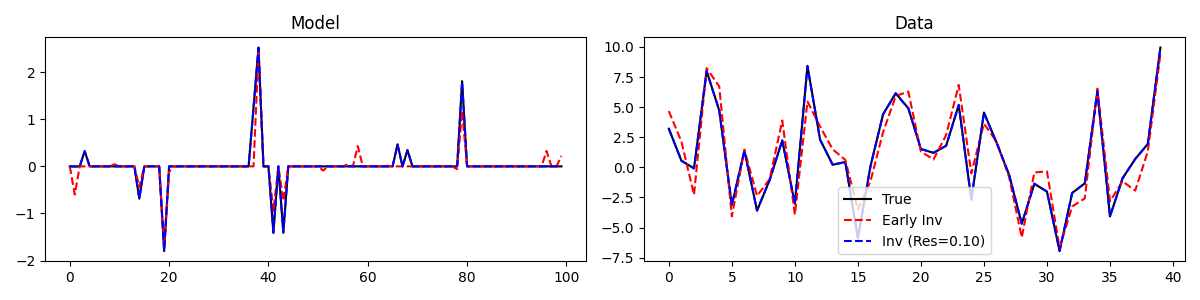
Note that at convergence the norm of the residual of the solution adheres to the EuclideanBall constraint