Note
Go to the end to download the full example code
Nonlinear inversion with box constraints#
In this tutorial we focus on a modification of the Quadratic program with box constraints tutorial where the quadratic function is replaced by a nonlinear function:
\[\mathbf{x} = \argmin_\mathbf{x} f(\mathbf{x}) \quad \text{s.t.} \quad \mathbf{x} \in \mathcal{I}_{\operatorname{Box}}\]
For this example we will use the well-known Rosenbrock function:
\[f(\mathbf{x}) = (a - x)^2 + b(y - x^2)^2\]
where \(\mathbf{x}=[x, y]\), \(a=1\), and \(b=10\).
We will learn how to handle nonlinear functionals in convex optimization, and
more specifically dive into the details of the
pyproximal.proximal.Nonlinear operator. This is a template operator
which must be subclassed and used for a specific functional. After doing so, we will
need to implement the following three method: func and grad and optimize.
As the names imply, the first method takes a model vector \(x\) as input and
evaluates the functional. The second method evaluates the gradient of the
functional with respect to \(x\). The third method implements an
optimization routine that solves the proximal operator of \(f\),
more specifically:
\[\prox_{\tau f} (\mathbf{x}) = \argmin_{\mathbf{y}} f(\mathbf{y}) + \frac{1}{2 \tau}\|\mathbf{y} - \mathbf{x}\|^2_2\]
Note that when creating the optimize method a user must use the gradient
of the augmented functional which is provided by the _gradprox built-in
method in pyproximal.proximal.Nonlinear class.
In this example, we will consider both the
pyproximal.optimization.primal.ProximalGradient and
pyproximal.optimization.primal.ADMM algorithms. The former solver
will simply use the grad method whilst the second solver relies on the
optimize method.
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pyproximal
plt.close('all')
Let’s start by defining the class for the nonlinear functional
def rosenbrock(x, y, a=1, b=10):
f = (a - x)**2 + b*(y - x**2)**2
return f
def rosenbrock_grad(x, y, a=1, b=10):
dfx = -2*(a - x) - 2*b*(y - x**2) * 2 * x
dfy = 2*b*(y - x**2)
return dfx, dfy
def contour_rosenbrock(x, y):
fig, ax = plt.subplots(figsize=(12, 6))
# Evaluate the function
x, y = np.meshgrid(x, y)
z = rosenbrock(x, y)
# Plot the surface.
surf = ax.contour(x, y, z, 200, cmap='gist_heat_r', vmin=-20, vmax=200,
antialiased=False)
fig.colorbar(surf, shrink=0.5, aspect=10)
return fig, ax
class Rosebrock(pyproximal.proximal.Nonlinear):
def setup(self, a=1, b=10, alpha=1.):
self.a, self.b = a, b
self.alpha = alpha
def fun(self, x):
return np.array(rosenbrock(x[0], x[1], a=self.a, b=self.b))
def grad(self, x):
return np.array(rosenbrock_grad(x[0], x[1], a=self.a, b=self.b))
def optimize(self):
self.solhist = []
sol = self.x0.copy()
for iiter in range(self.niter):
x1, x2 = sol
dfx1, dfx2 = self._gradprox(sol, self.tau)
x1 -= self.alpha * dfx1
x2 -= self.alpha * dfx2
sol = np.array([x1, x2])
self.solhist.append(sol)
self.solhist = np.array(self.solhist)
return sol
We can now setup the problem and solve it without constraints using a simple gradient descent with fixed-step size (of course we could choose any other solver)
Let’s now define the box constraint
xbound = np.arange(-1.5, 1.5, 0.01)
ybound = np.arange(-0.5, 1.5, 0.01)
X, Y = np.meshgrid(xbound, ybound, indexing='ij')
xygrid = np.vstack((X.ravel(), Y.ravel()))
lower = 0.6
upper = 1.2
indic = (xygrid > lower) & (xygrid < upper)
indic = indic[0].reshape(xbound.size, ybound.size) & \
indic[1].reshape(xbound.size, ybound.size)
We now solve the constrained optimization using the Proximal gradient solver
fnl = Rosebrock(niter=20, x0=np.zeros(2), warm=True)
fnl.setup(1, 10, alpha=0.02)
ind = pyproximal.proximal.Box(lower, upper)
def callback(x):
xhist.append(x)
x0 = np.array([0, 0])
xhist = [x0,]
xinv_pg = pyproximal.optimization.primal.ProximalGradient(fnl, ind,
tau=0.001,
x0=x0, epsg=1.,
niter=5000, show=True,
callback=callback)
xhist_pg = np.array(xhist)
Accelerated Proximal Gradient
---------------------------------------------------------
Proximal operator (f): <class '__main__.Rosebrock'>
Proximal operator (g): <class 'pyproximal.proximal.Box.Box'>
tau = 0.001 beta=5.000000e-01
epsg = 1.0 niter = 5000
niterback = 100 acceleration = None
Itn x[0] f g J=f+eps*g tau
1 6.00000e-01 7.360e-01 0.000e+00 7.360e-01 1.000e-03
2 6.06560e-01 6.934e-01 0.000e+00 6.934e-01 1.000e-03
3 6.12978e-01 6.527e-01 0.000e+00 6.527e-01 1.000e-03
4 6.19250e-01 6.138e-01 0.000e+00 6.138e-01 1.000e-03
5 6.25375e-01 5.768e-01 0.000e+00 5.768e-01 1.000e-03
6 6.31350e-01 5.415e-01 0.000e+00 5.415e-01 1.000e-03
7 6.37174e-01 5.080e-01 0.000e+00 5.080e-01 1.000e-03
8 6.42844e-01 4.763e-01 0.000e+00 4.763e-01 1.000e-03
9 6.48361e-01 4.463e-01 0.000e+00 4.463e-01 1.000e-03
10 6.53722e-01 4.180e-01 0.000e+00 4.180e-01 1.000e-03
501 8.25975e-01 3.089e-02 1.000e+00 1.031e+00 1.000e-03
1001 8.64935e-01 1.859e-02 1.000e+00 1.019e+00 1.000e-03
1501 8.93688e-01 1.151e-02 1.000e+00 1.012e+00 1.000e-03
2001 9.15492e-01 7.269e-03 1.000e+00 1.007e+00 1.000e-03
2501 9.32340e-01 4.658e-03 1.000e+00 1.005e+00 1.000e-03
3001 9.45538e-01 3.017e-03 1.000e+00 1.003e+00 1.000e-03
3501 9.55982e-01 1.971e-03 1.000e+00 1.002e+00 1.000e-03
4001 9.64309e-01 1.295e-03 1.000e+00 1.001e+00 1.000e-03
4501 9.70988e-01 8.557e-04 1.000e+00 1.001e+00 1.000e-03
4992 9.76284e-01 5.718e-04 1.000e+00 1.001e+00 1.000e-03
4993 9.76294e-01 5.713e-04 1.000e+00 1.001e+00 1.000e-03
4994 9.76303e-01 5.709e-04 1.000e+00 1.001e+00 1.000e-03
4995 9.76313e-01 5.704e-04 1.000e+00 1.001e+00 1.000e-03
4996 9.76323e-01 5.699e-04 1.000e+00 1.001e+00 1.000e-03
4997 9.76332e-01 5.695e-04 1.000e+00 1.001e+00 1.000e-03
4998 9.76342e-01 5.690e-04 1.000e+00 1.001e+00 1.000e-03
4999 9.76352e-01 5.685e-04 1.000e+00 1.001e+00 1.000e-03
5000 9.76361e-01 5.681e-04 1.000e+00 1.001e+00 1.000e-03
Total time (s) = 0.10
---------------------------------------------------------
And using the ADMM solver
ADMM
---------------------------------------------------------
Proximal operator (f): <class '__main__.Rosebrock'>
Proximal operator (g): <class 'pyproximal.proximal.Box.Box'>
tau = 1.000000e+00 niter = 30
Itn x[0] f g J = f + g
1 4.05651e-01 3.591e-01 0.000e+00 3.591e-01
2 7.23299e-01 7.695e-02 0.000e+00 7.695e-02
3 8.48264e-01 2.309e-02 1.000e+00 1.023e+00
4 9.05255e-01 8.986e-03 1.000e+00 1.009e+00
5 9.17660e-01 6.910e-03 1.000e+00 1.007e+00
6 9.04521e-01 9.516e-03 1.000e+00 1.010e+00
7 9.17031e-01 7.010e-03 1.000e+00 1.007e+00
8 9.28365e-01 5.222e-03 1.000e+00 1.005e+00
9 9.38010e-01 3.910e-03 1.000e+00 1.004e+00
10 9.46245e-01 2.939e-03 1.000e+00 1.003e+00
13 9.64619e-01 1.273e-03 1.000e+00 1.001e+00
16 9.76484e-01 5.622e-04 1.000e+00 1.001e+00
19 9.84273e-01 2.514e-04 1.000e+00 1.000e+00
22 9.89439e-01 1.133e-04 1.000e+00 1.000e+00
23 9.90746e-01 8.702e-05 1.000e+00 1.000e+00
24 9.91889e-01 6.685e-05 1.000e+00 1.000e+00
25 9.92889e-01 5.137e-05 1.000e+00 1.000e+00
26 9.93763e-01 3.950e-05 1.000e+00 1.000e+00
27 9.94528e-01 3.038e-05 1.000e+00 1.000e+00
28 9.95194e-01 2.337e-05 1.000e+00 1.000e+00
29 9.95771e-01 1.801e-05 1.000e+00 1.000e+00
30 9.96261e-01 1.399e-05 1.000e+00 1.000e+00
Total time (s) = 0.01
---------------------------------------------------------
To conclude it is important to notice that whilst we implemented a vanilla gradient descent inside the optimize method, any more advanced solver can be used (here for example we will repeat the same exercise using L-BFGS from scipy.
class Rosebrock_lbfgs(Rosebrock):
def optimize(self):
def callback(x):
self.solhist.append(x)
self.solhist = []
self.solhist.append(self.x0)
sol = sp.optimize.minimize(lambda x: self._funprox(x, self.tau),
x0=self.x0,
jac=lambda x: self._gradprox(x, self.tau),
method='L-BFGS-B', callback=callback,
options=dict(maxiter=15))
sol = sol.x
self.solhist = np.array(self.solhist)
return sol
fnl = Rosebrock_lbfgs(niter=20, x0=np.zeros(2), warm=True)
fnl.setup(1, 10, alpha=0.02)
x0 = np.array([0, 0])
xhist = [x0,]
xinv_admm_lbfgs = pyproximal.optimization.primal.ADMM(fnl, ind,
tau=1.,
x0=x0,
niter=30, show=True,
callback=callback)
xhist_admm_lbfgs = np.array(xhist)
ADMM
---------------------------------------------------------
Proximal operator (f): <class '__main__.Rosebrock_lbfgs'>
Proximal operator (g): <class 'pyproximal.proximal.Box.Box'>
tau = 1.000000e+00 niter = 30
Itn x[0] f g J = f + g
1 5.56967e-01 1.985e-01 0.000e+00 1.985e-01
2 9.17533e-01 6.890e-03 1.000e+00 1.007e+00
3 8.86812e-01 1.318e-02 1.000e+00 1.013e+00
4 9.05365e-01 9.178e-03 1.000e+00 1.009e+00
5 9.34197e-01 4.406e-03 1.000e+00 1.004e+00
6 9.53886e-01 2.163e-03 1.000e+00 1.002e+00
7 9.67451e-01 1.077e-03 1.000e+00 1.001e+00
8 9.76913e-01 5.418e-04 1.000e+00 1.001e+00
9 9.83569e-01 2.744e-04 1.000e+00 1.000e+00
10 9.88278e-01 1.396e-04 1.000e+00 1.000e+00
13 9.95709e-01 1.871e-05 1.000e+00 1.000e+00
16 9.98421e-01 2.534e-06 1.000e+00 1.000e+00
19 9.99414e-01 3.483e-07 1.000e+00 1.000e+00
22 9.99784e-01 4.760e-08 1.000e+00 1.000e+00
23 9.99870e-01 1.687e-08 1.000e+00 1.000e+00
24 9.99873e-01 1.661e-08 1.000e+00 1.000e+00
25 9.99872e-01 1.635e-08 1.000e+00 1.000e+00
26 9.99875e-01 1.609e-08 1.000e+00 1.000e+00
27 9.99874e-01 1.581e-08 1.000e+00 1.000e+00
28 9.99877e-01 1.554e-08 1.000e+00 1.000e+00
29 9.99877e-01 1.517e-08 1.000e+00 1.000e+00
30 9.99879e-01 1.484e-08 1.000e+00 1.000e+00
Total time (s) = 0.02
---------------------------------------------------------
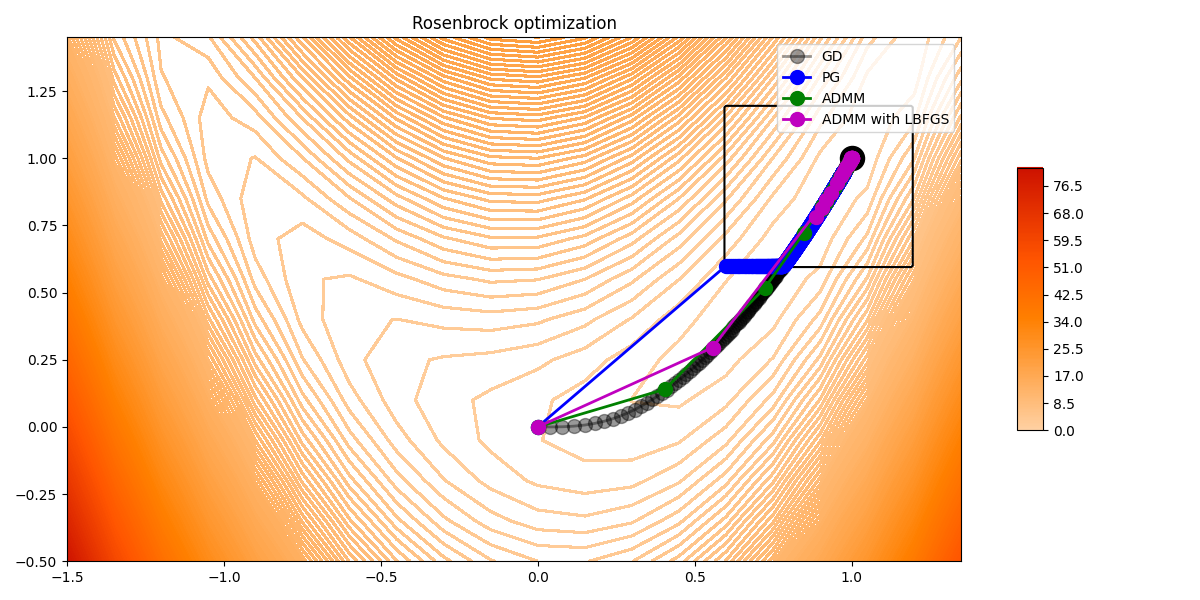
Finally let’s compare the results.
fig, ax = contour_rosenbrock(x, y)
steps = np.array(steps)
ax.contour(X, Y, indic, colors='k')
ax.scatter(1, 1, c='k', s=300)
ax.plot(steps[:, 0], steps[:, 1], '.-k', lw=2, ms=20, alpha=0.4, label='GD')
ax.plot(xhist_pg[:, 0], xhist_pg[:, 1], '.-b', ms=20, lw=2, label='PG')
ax.plot(xhist_admm[:, 0], xhist_admm[:, 1], '.-g', ms=20, lw=2, label='ADMM')
ax.plot(xhist_admm_lbfgs[:, 0], xhist_admm_lbfgs[:, 1], '.-m', ms=20, lw=2,
label='ADMM with LBFGS')
ax.set_title('Rosenbrock optimization')
ax.legend()
ax.set_xlim(x[0], x[-1])
ax.set_ylim(y[0], y[-1])
fig.tight_layout()
Total running time of the script: (0 minutes 0.603 seconds)
